
分析 (1)由真数大于零得$\frac{1+x}{1-x}$>0,即(1+x)(1-x)>0,解得-1<x<1.
(2)利用对数函数的单调性将f(x)>0转化为$\frac{1+x}{1-x}$>1,从而解决问题.
解答 解:(1)由f(x)=ln$\frac{1+x}{1-x}$有意义得
$\frac{1+x}{1-x}$>0,即(1+x)(1-x)>0,
解得-1<x<1.
∴f(x)的定义域为(-1,1).
(2)∵f(x)>0,即ln$\frac{1+x}{1-x}$>0,
∴$\frac{1+x}{1-x}$>1.
∵x∈(-1,1),∴1-x>0,
∴1+x>1-x,解得x>0.
∵x∈(-1,1),∴0<x<1.
∴使函数f(x)>0的x的取值范围是(0,1).
点评 本题主要考查了对数函数的定义域、对数不等式及分式不等式的解法,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
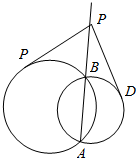 如图,两圆相交于A、B两点,P为两圆公共弦AB上任一点,从P引两圆的切线PC、PD,若PC=2$\sqrt{2}$cm,则PD=2$\sqrt{2}$cm.
如图,两圆相交于A、B两点,P为两圆公共弦AB上任一点,从P引两圆的切线PC、PD,若PC=2$\sqrt{2}$cm,则PD=2$\sqrt{2}$cm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
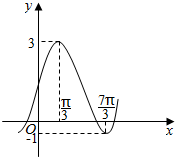 已知平面向量$\overrightarrow{a}$=(sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$,cos2$\frac{ωx}{2}$),$\overrightarrow{b}$=(cosφ,sinφ),函数f(x)=2A($\overrightarrow{a}$•$\overrightarrow{b}$)-Asinφ+k(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知平面向量$\overrightarrow{a}$=(sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$,cos2$\frac{ωx}{2}$),$\overrightarrow{b}$=(cosφ,sinφ),函数f(x)=2A($\overrightarrow{a}$•$\overrightarrow{b}$)-Asinφ+k(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2-2x-3 | B. | f(x)=x2+2x-3 | C. | f(x)=x2-2x+3 | D. | f(x)=x2+2x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com