
【题目】已知定义在R上的函数y=f(x),满足f(2)=0,函数y=f(x+1)的图象关于点(-1,0)中心对称,且对任意的负数x1,x2(x1≠x2),![]() 恒成立,则不等式f(x)<0的解集为____.
恒成立,则不等式f(x)<0的解集为____.
【答案】(-∞,-2)∪(0,2)
【解析】
根据条件判断函数f(x)是奇函数,结合不等式的性质,构造函数h(x)=x2107f(x),研究函数h(x)的奇偶性和取值情况,进行求解即可.
∵函数y=f(x+1)的图象关于点(-1,0)中心对称,
∴函数y=f(x)的图象关于点(0,0)中心对称,即函数f(x)是奇函数,
对对任意的负数x1,x2(x1≠x2),![]() 恒成立,
恒成立,
不妨设x1<x2,则x12107f(x1)-x22107f(x2)>0,
设h(x)=x2107f(x),则不等式等价为h(x1)>h(x2),且函数h(x)是偶函数,
即h(x)在(-∞,0)上为减函数,∵f(2)=0,∴h(2)=22107f(2)=0,
则当x>0时,不等式f(x)<0等价为不等式x2107f(x)<0,即h(x)<0
当x<0时,不等式f(x)<0等价为不等式x2107f(x)>0,即h(x)>0,
当x>0时,由h(x)<0得0<x<2,
当x<0时,由h(x)>0得x<-2,
即f(x)<0的解集为(-∞,-2)∪(0,2),
故答案为:(-∞,-2)∪(0,2).


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知0<a<b,且a+b=1,则下列不等式中正确的是( )
A.log2a>0
B.2a﹣b< ![]()
C.log2a+log2b<﹣2
D.2( ![]() +
+ ![]() )<
)< ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学在“三关心”(即关心家庭、关心学校、关心社会)的专题中,对个税起征点问题进行了学习调查.学校决定从高一年级800人,高二年级1000人,高三年级800人中按分层抽样的方法共抽取13人进行谈话,其中认为个税起征点为3000元的有3人,认为个税起征点为4000元的有6人,认为个税起征点为 5000元的有4人.
(1)求高一年级、高二年级、高三年级分别抽取多少人?
(2)从13人中选出3人,求至少有1人认为个税起征点为4000元的概率;
(3)记从13人中选出3人中认为个税起征点为4000元的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 和
和![]() 在
在![]() 的图象如图所示:
的图象如图所示:
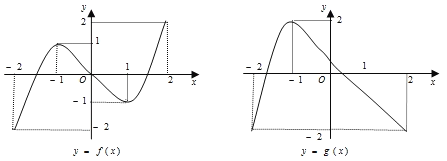
给出下列四个命题:
(1)方程![]() 有且仅有6个根;
有且仅有6个根;
(2)方程![]() 有且仅有3个根;
有且仅有3个根;
(3)方程![]() 有且仅有5个根;
有且仅有5个根;
(4)方程![]() 有且仅有4个根.
有且仅有4个根.
其中正确命题的个数是( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.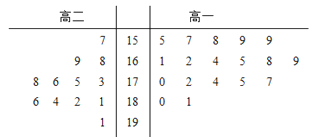
(1)如果从所有运动员中用分层抽样抽取“合格”与“不合格”的人数共10人,问就抽取“合格”人数是多少?
(2)若从所有“合格”运动员中选取2名,用X表示所选运动员来自高一队的人数,试写出X的分布图,并求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,a1=2,b1=4且an , bn , an+1成等差数列,bn , an+1 , bn+1成等比数列(n∈N*)
(1)求a2 , a3 , a4及b2 , b3 , b4;由此归纳出{an},{bn}的通项公式,并证明你的结论.
(2)若cn=log2(![]() ),Sn=c1+c2+…+cn , 试问是否存在正整数m,使Sm≥5,若存在,求最小的正整数m.
),Sn=c1+c2+…+cn , 试问是否存在正整数m,使Sm≥5,若存在,求最小的正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB=![]() .
.
证明:平面ADE⊥平面ACD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
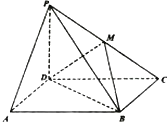
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com