
(本大题满分10分)设函数f(x)=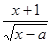 (a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。
(a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。
a≤-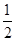
【解析】
试题分析:首先要使函数有意义,则a≤x。而考虑所给的题设,只需要最大限度地让函数在(0,+∞)有意义即可,所以a≤0。对f(x)求导并令其≥0,整理后得:[x-(2a+1)] 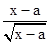 ≥0
≥0
由于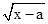 在a≤0时始终有意义且大于0,因此只需讨论[x-(2a+1)](x-a)≥0 .........①
在a≤0时始终有意义且大于0,因此只需讨论[x-(2a+1)](x-a)≥0 .........①
(1)若2a+1≥a,即a≥-1。①解为x≤a或x≥2a+1,所以令2a+1≤0即可,得到a≤-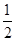
(2)若2a+1<a,即a<-1。①解为x<2a+1或x>a,所以令a≤0即可
综上所述,a的取值范围是(-∞,-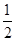 ]。
]。
考点:本题主要考查利用导数研究函数的单调性,一元二次不等式的解法。
点评:已知函数的单调区间,求参数,往往利用函数的导数不小于0。解答本题时,分类讨论是关键。


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
(本大题满分10分).能否将下列数组中的数填入3×3的方格表,每个小方格中填一个数,使得每行、每列、两条对角线上的3个数的乘积都相等?若能,请给出一种填法;若不能,请给予证明.(Ⅰ)2,4,6,8,12,18,24,36,48; (Ⅱ)2,4,6,8,12,18,24,36,72.
查看答案和解析>>
科目:高中数学 来源:2010年浙东北三校高一下学期期中联考数学 题型:解答题
(本大题满分10分)已知函数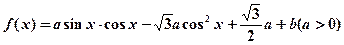 .
.
(Ⅰ)求函数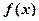 的单调递减区间;
的单调递减区间;
(Ⅱ)已知函数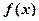 在区间
在区间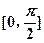 上的最小值是
上的最小值是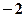 ,最大值是
,最大值是 ,求实数
,求实数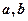 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010年浙东北三校高一下学期期中联考数学 题型:解答题
(本大题满分10分)是否存在实数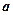 ,使函数
,使函数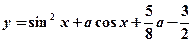 在闭区间
在闭区间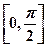 上的最大值为
上的最大值为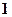 ?若存在,求出对应的
?若存在,求出对应的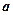 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com