
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() 底面
底面![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 上一点.
上一点.
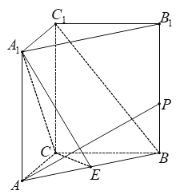
(1)求证: ![]()
![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() ,若
,若![]()
![]()
![]() ,写出
,写出![]() 的值(不需写过程).
的值(不需写过程).
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)证明![]()
![]() 平面
平面![]() ,只要在面
,只要在面![]() 内找到一条直线与
内找到一条直线与![]() 平行;
平行;
(2)以![]() ,
,![]() ,
,![]() 分别为x,y,z轴建立空间直角坐标系,写出两个面的法向量,再求法向量的夹角,结合图形发现二面角的平面角为钝角,从而求得二面角的余弦值。
分别为x,y,z轴建立空间直角坐标系,写出两个面的法向量,再求法向量的夹角,结合图形发现二面角的平面角为钝角,从而求得二面角的余弦值。
(3)由![]()
![]()
![]() ,
,![]()
![]()
![]() 可证得
可证得![]()
![]() 平面
平面![]() ,进而得到
,进而得到![]()
![]()
![]() ,再利用相似得到
,再利用相似得到![]() 为
为![]() 中点。
中点。
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
因为四边形![]() 为矩形,
为矩形,![]() ,
,![]() 为对角线,
为对角线,
所以![]() 为
为![]() 中点,又因为
中点,又因为![]() 为
为![]() 中点,
中点,
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]() .
.
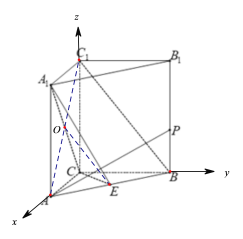
(2)因为![]() 底面
底面![]() ,所以
,所以![]() 底面
底面![]() ,
,
又![]() ,所以以
,所以以![]() ,
,![]() ,
,![]() 分别为x,y,z轴建立空间直角坐标系.
分别为x,y,z轴建立空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则有
,则有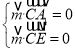 ,即
,即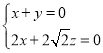
令![]() ,则
,则![]() .
.
由题意![]() 底面
底面![]() ,所以
,所以![]() 为平面
为平面![]() 的法向量,
的法向量,
所以![]() ,又由图可知二面角
,又由图可知二面角![]() 为钝二面角,
为钝二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() 。
。
(3)![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() 设圆C的半径为1,圆心在直线l上.
设圆C的半径为1,圆心在直线l上.
(1)若圆心C也在直线![]() 上,过点
上,过点![]() 作圆C的切线,求切线的方程;
作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使得![]() ,求圆心C的横坐标
,求圆心C的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,有下列四个命题:
,有下列四个命题:
①若![]() 是奇函数,则
是奇函数,则![]() 的图象关于点
的图象关于点![]() 对称;
对称;
②若对![]() ,有
,有![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③若对![]() ,有
,有![]() ,则
,则![]() 的图象关于点
的图象关于点![]() 对称;
对称;
④函数![]() 与函数
与函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
其中正确命题的序号为__________.(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业2018年招聘员工,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性 应聘人数 | 男性 录用人数 | 男性 录用比例 | 女性 应聘人数 | 女性 录用人数 | 女性 录用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
总计 | 533 | 264 |
| 467 | 169 |
|
(1)从表中所有应聘人员中随机选择1人,试估计此人被录用的概率;
(2)从应聘![]() 岗位的6人中随机选择2人.记
岗位的6人中随机选择2人.记![]() 为这2人中被录用的人数,求
为这2人中被录用的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于
各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于![]() ),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在如图所示的多面体中,四边形![]() 和
和![]() 都为矩形。
都为矩形。

(Ⅰ)若![]() ,证明:直线
,证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 平面
平面![]() ?请证明你的结论。
?请证明你的结论。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣3≤0},B={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R}.
(1)若A∪B=A,求实数m的取值;
(2)若A∩B={x|0≤x≤3},求实数m的值;
(3)若A![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 上存在两点
上存在两点![]() ,椭圆
,椭圆![]() 上存在两个
上存在两个![]() 点满足:
点满足:![]() 三点共线,
三点共线,![]() 三点共线,且
三点共线,且![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:

(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com