
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线:
,直线:![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点,![]() .
.
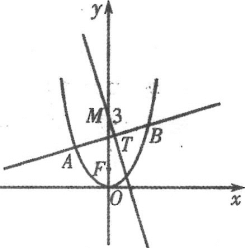
(1)若![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,证明:
,证明:![]() 为定值;
为定值;
(2)求![]() 面积的最大值.
面积的最大值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设A(x1,y1),B(x2,y2),联立直线与抛物线方程可得:x1+x2=4k,即可求得AB的中点坐标为T(2k,1),问题得证。
(2)由弦长公式得:![]() ,再求得点M到直线
,再求得点M到直线![]() 距离为
距离为![]() ,由(1)可得
,由(1)可得![]() ,即可得
,即可得![]() ,记:
,记:![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,利用导数即可求得
,利用导数即可求得![]() ,问题得解。
,问题得解。
(1)证明:联立![]() ,消去y得,x2-4kx-4b=0,
,消去y得,x2-4kx-4b=0,
△=16k2+16b>0,即k2+b>0,
设A(x1,y1),B(x2,y2),由韦达定理得x1+x2=4k,x1x2=-4b,
因为|AF|+|BF|=4,
由抛物线定义得y1+1+y2+1=4,得y1+y2=2,
所以AB的中点坐标为T(2k,1),
所以![]() ,
,
所以![]() .
.
(2)由(1)得|x1-x2|2=(x1+x2)2-4x1x2=16(k2+b),
![]() ,
,
设点M到直线![]() 距离为d,
距离为d,
则![]() ,
,
而由(1)知,y1+y2=kx1+b+kx2+b=k(x1+x2)+2b=4k2+2b=2,
即2k2+b=1,即b=1-2k2,
由△=16k2+16b>0,得0<k2<1,
所以![]()
![]() ,
,
记:![]()
令t=k2,0<t<1,则![]()
记![]()
![]() f(t)=(1+t)2(1-t)=1+t-t2-t3,0<t<1,
f(t)=(1+t)2(1-t)=1+t-t2-t3,0<t<1,
f'(t)=1-2t-3t2=(t+1)(-3t+1),
当![]() 时,f'(t)>0,f(t)为增函数;
时,f'(t)>0,f(t)为增函数;
当![]() 时,f'(t)<0,f(t)为减函数;
时,f'(t)<0,f(t)为减函数;
当![]() ,
,![]() ,
,
所以,S△ABM的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,平面四边形ABCD中,E、F是AD、BD中点,AB=AD=CD=2, BD=2![]() ,∠BDC=90°,将△ABD沿对角线BD折起至△
,∠BDC=90°,将△ABD沿对角线BD折起至△![]() ,使平面
,使平面![]() ⊥平面BCD,则四面体
⊥平面BCD,则四面体![]() 中,下列结论不正确是 ( )
中,下列结论不正确是 ( )
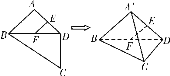
A. EF∥平面![]()
B. 异面直线CD与![]() 所成的角为90°
所成的角为90°
C. 异面直线EF与![]() 所成的角为60°
所成的角为60°
D. 直线![]() 与平面BCD所成的角为30°
与平面BCD所成的角为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,点
倍,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若过椭圆的左焦点的直线![]() 与椭圆
与椭圆![]() 相交所得弦长为
相交所得弦长为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(3)过点![]() 的任意直线与椭圆
的任意直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,设点
两点,设点![]() 、
、![]() 到直线
到直线![]() :
:![]() 的距离分别为
的距离分别为![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 |
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市12月1日-20日AQI指数变化趋势:

下列叙述正确的是( )
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占![]()
C.该市12月的前半个月的空气质量越来越好
D.总体来说,该市12月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是一种古老的中国传统智力玩具,是由七块板组成的.而这七块板可拼成许多图形,例如:三角形、不规则多边形、各种人物、动物、建筑物等,清陆以湉《冷庐杂识》写道:近又有七巧图,其式五,其数七,其变化之式多至千余.在18世纪,七巧板流传到了国外,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.若用七巧板拼成一只雄鸡,在雄鸡平面图形上随机取一点,则恰好取自雄鸡鸡尾(阴影部分)的概率为( )
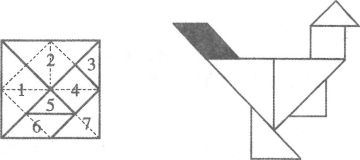
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①如果平面![]() 外一条直线
外一条直线![]() 与平面
与平面![]() 内一条直线
内一条直线![]() 平行,那么
平行,那么![]() ;
;
②过空间一定点有且只有一条直线与已知平面垂直;
③如果一条直线垂直于一个平面内的无数条直线,那么这条直线与这个平面垂直;
④若两个相交平面都垂直于第三个平面,则这两个平面的交线垂直于第三个平面.
其中真命题的序号为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代研究表明,体脂率![]() (体脂百分数)是衡量人体体重与健康程度的一个标准.为分析体脂率
(体脂百分数)是衡量人体体重与健康程度的一个标准.为分析体脂率![]() 对人体总胆固醇
对人体总胆固醇![]() 的影响,从女性志愿者中随机抽取12名志愿者测定其体脂率
的影响,从女性志愿者中随机抽取12名志愿者测定其体脂率![]() 值及总胆固醇
值及总胆固醇![]() 指标值(单位:mmol/L),得到的数据如表所示:
指标值(单位:mmol/L),得到的数据如表所示:
![]()
(1)利用表中的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请用相关系数
的关系?请用相关系数![]() 加以说明.(若
加以说明.(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)求出![]() 与
与![]() 的线性回归方程,并预测总胆固醇
的线性回归方程,并预测总胆固醇![]() 指标值为9.5时,对应的体脂率
指标值为9.5时,对应的体脂率![]() 值
值![]() 为多少?(上述数据均要精确到0.1)
为多少?(上述数据均要精确到0.1)
(3)医学研究表明,人体总胆固醇![]() 指标值
指标值![]() 服从正态分布
服从正态分布![]() ,若人体总胆固醇
,若人体总胆固醇![]() 指标值
指标值![]() 在区间
在区间![]() 之外,说明人体总胆固醇异常,该志愿者需作进一步医学观察.现用样本的
之外,说明人体总胆固醇异常,该志愿者需作进一步医学观察.现用样本的![]() 作为
作为![]() 的估计值,用样本的标准差
的估计值,用样本的标准差![]() 作为
作为![]() 的估计值,从这12名女志愿者中随机抽4人,记需作进一步医学观察的人数为
的估计值,从这12名女志愿者中随机抽4人,记需作进一步医学观察的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:参考公式:相关系数 ,
, ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络平台从购买该平台某课程的客户中,随机抽取了100位客户的数据,并将这100个数据按学时数,客户性别等进行统计,整理得到如表:
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
(1)根据上表估计男性客户购买该课程学时数的平均值(同一组中的数据用该组区间的中点值作代表,结果保留小数点后两位);
(2)从这100位客户中,对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人,再从这7人中随机抽取2人,求这2人购买的学时数都不低于15的概率.
(3)将购买该课程达到25学时及以上者视为“十分爱好该课程者”,25学时以下者视,为“非十分爱好该课程者”.请根据已知条件完成以下![]() 列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com