
【题目】已知函数![]() (
(![]() ),曲线
),曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(Ⅱ)若函数![]() 有两个不同的零点
有两个不同的零点![]() ,
, ![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(I)切线与直线![]() 垂直,即在该点导数为
垂直,即在该点导数为![]() ,利用导数为
,利用导数为![]() 列方程可求得
列方程可求得![]() 的值.利用导数判断函数的单调区间,得函数在
的值.利用导数判断函数的单调区间,得函数在![]() 上为减函数,故
上为减函数,故![]() ,化简得
,化简得![]() .(II)不妨设
.(II)不妨设![]() 因为
因为![]() ,
,
所以化简得![]() ,
, ![]() ,两式相加和相减,利用分析法分析要证明的不等式,将不等式转化为证
,两式相加和相减,利用分析法分析要证明的不等式,将不等式转化为证![]() ,利用换元法和导数作为工具,可证明上述不等式成立.
,利用换元法和导数作为工具,可证明上述不等式成立.
试题解析:
解:(Ⅰ)依题意得, 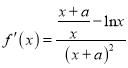 ,
,
所以![]() ,又由切线方程可得
,又由切线方程可得![]() ,即
,即![]() ,解得
,解得![]() .
.
此时![]() ,
, ![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() .
.
所以![]() ,即
,即![]() .
.
![]()
![]() ,
, ![]() .
.
(Ⅱ)证明:不妨设![]() 因为
因为![]() ,
,
所以化简得![]() ,
, ![]() .
.
可得![]() ,
, ![]() ,
,
要证明, ![]() 即证明
即证明![]() ,也就是
,也就是![]() .
.
因为![]() ,所以即证
,所以即证![]() ,
,
即![]() ,令
,令![]() ,则
,则![]() ,即证
,即证![]() .
.
令![]() (
(![]() ).由
).由![]()
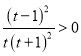 ,
,
故函数![]() 在
在![]() 是增函数,所以
是增函数,所以![]() ,即
,即![]() 得证.
得证.
所以![]() .
.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(1)设月用电x度时,应交电费y元,写出y关于x的函数关系式;
(2)小明家第一季度缴纳电费情况如下:问小明家第一季度共用电多少度?
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式(1-a)x2-4x+6>0的解集是{x|-3<x<1}.
(1)解不等式2x2+(2-a)x-a>0;
(2)b为何值时,ax2+bx+3≥0的解集为R.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列给出四组函数,表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=x,g(x)= ![]()
D.f(x)=1,g(x)=x0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4, 则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标 (x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标 (x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中, 随机抽取2件产品,
(ⅰ) 用产品编号列出所有可能的结果;
(ⅱ) 设事件B为“在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
(1)求A,(RA)∩B;
(2)若A∪C=R,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com