
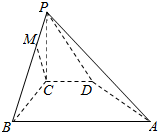
 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.求证:
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.求证:分析 根据题意,建立空间直角坐标系O-xyz,C为坐标原点O,
(1)要证CM∥面PAD,只需求出向量$\overrightarrow{CM}$与面PAD内的向量$\overrightarrow{DP}$、$\overrightarrow{DA}$共面即可.
(2)过B作BE⊥PA,E为垂足.要证面PAB⊥面PAD,只需证明面PAB内的向量$\overrightarrow{BE}$垂直面PAD内的直线PA、DA即可.
解答 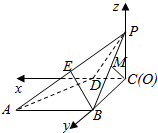 解:如图,建立空间直角坐标系O-xyz,C为坐标原点O,
解:如图,建立空间直角坐标系O-xyz,C为坐标原点O,
(1)证明:如图,建立空间直角坐标系.
∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABC所成的角,即∠PBC=30°.
∵|PC|=2,∴|BC|=2$\sqrt{3}$,|PB|=4.
得D(1,0,0)、B(0,2$\sqrt{3}$,0)、
A(4,2$\sqrt{3}$,0)、P(0,0,2).
∵PB=4PM,∴|MB|=3|PM|,
∴|PM|=1,M(0,$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),$\overrightarrow{CM}$=(0,$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),
$\overrightarrow{DP}$=(-1,0,2),$\overrightarrow{DA}$=(3,2$\sqrt{3}$,0).
设$\overrightarrow{CM}$=x$\overrightarrow{DP}$+y$\overrightarrow{DA}$(x、y∈R),
则(0,$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$)=x(-1,0,2)+y(3,2$\sqrt{3}$,0)⇒x=$\frac{3}{4}$且y=$\frac{1}{4}$,
∴$\overrightarrow{CM}$=$\frac{3}{4}$$\overrightarrow{DP}$+$\frac{1}{4}$$\overrightarrow{DA}$.
∴$\overrightarrow{CM}$、$\overrightarrow{DP}$、$\overrightarrow{DA}$共面.
又∵C∉平面PAD,故CM∥平面PAD.
(2)证明:过B作BE⊥PA,E为垂足.
∵|PB|=|AB|=4,∴E为PA的中点.
∴E(2,$\sqrt{3}$,1),$\overrightarrow{BE}$=(2,-$\sqrt{3}$,1).
又∵$\overrightarrow{BE}$•$\overrightarrow{DA}$=(2,-$\sqrt{3}$,1)•(3,2$\sqrt{3}$,0)=0,
∴$\overrightarrow{BE}$⊥$\overrightarrow{DA}$,即BE⊥DA.
而BE⊥PA,∴BE⊥面PAD.
∵BE?面PAB,∴面PAB⊥面PAD.
点评 本题主要考查空间直角坐标系的概念、空间点和向量的坐标表示以及用向量法证明平行关系,同时考查向量研究空间图形的数学思想方法.突破点在于求出相关的向量所对应的坐标.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
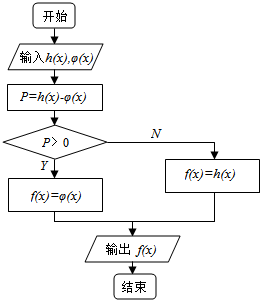 函数f(x)的定义由程序框图给出,程序运行时,输入h(x)=($\frac{1}{2}$)x,φ(x)=log2x,则f($\frac{1}{2}$)+f(4)的值为-$\frac{15}{16}$.
函数f(x)的定义由程序框图给出,程序运行时,输入h(x)=($\frac{1}{2}$)x,φ(x)=log2x,则f($\frac{1}{2}$)+f(4)的值为-$\frac{15}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 4+4$\sqrt{3}$ | C. | 4+4$\sqrt{2}$ | D. | 4+8$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com