
【题目】已知动点![]() 到定直线
到定直线![]() :
:![]() 的距离比到定点
的距离比到定点![]() 的距离大2.
的距离大2.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)在![]() 轴正半轴上,是否存在某个确定的点
轴正半轴上,是否存在某个确定的点![]() ,过该点的动直线
,过该点的动直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,使得
两点,使得![]() 为定值.如果存在,求出点
为定值.如果存在,求出点![]() 坐标;如果不存在,请说明理由.
坐标;如果不存在,请说明理由.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】以下四个命题中错误的是( )
A.样本频率分布直方图中的小矩形的面积就是对应组的频率
B.回归直线过样本点的中心![]()
C.若样本![]() 的平均数是2,方差是2,则数据
的平均数是2,方差是2,则数据![]() 的平均数是4,方差是4
的平均数是4,方差是4
D.抛掷一颗质地均匀的骰子,事件“向上点数不大于3”和事件“向上点数不小于4”是对立事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三理科班共有![]() 名同学参加某次考试,从中随机挑出
名同学参加某次考试,从中随机挑出![]() 名同学,他们的数学成绩
名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 |
|
|
|
|
|
物理成绩 |
|
|
|
|
|
(1)数据表明![]() 与
与![]() 之间有较强的线性关系,求
之间有较强的线性关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)本次考试中,规定数学成绩达到![]() 分为优秀,物理成绩达到
分为优秀,物理成绩达到![]() 分为优秀.若该班数学优秀率与物理优秀率分别为
分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的
,且除去抽走的![]() 名同学外,剩下的同学中数学优秀但物理不优秀的同学共有
名同学外,剩下的同学中数学优秀但物理不优秀的同学共有![]() 人,请写出
人,请写出![]() 列联表,判断能否在犯错误的概率不超过
列联表,判断能否在犯错误的概率不超过![]() 的前提下认为数学优秀与物理优秀有关?
的前提下认为数学优秀与物理优秀有关?
参考数据: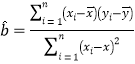 ,
,![]() ;
;![]() ,
,![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
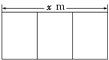
【题目】 为了净化广州水系,拟在小清河建一座平面图(如图所示)为矩形且面积为200 m2的三级污水处理池,由于地形限制,长、宽都不能超过16 m,如果池外壁建造单价为400元/m2,中间两条隔墙建造单价为248元/m2,池底建造单价为80元/m2(池壁厚度忽略不计,且池无盖).
(1)写出总造价y(元)与x的函数关系式,并指出定义域;
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低,并求最低造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算,当某产品促销费用为x(万元)时,销售量t(万件)满足![]() (其中
(其中![]() ,
,![]() ).现假定产量与销售量相等,已知生产该产品t万件还需投入成本
).现假定产量与销售量相等,已知生产该产品t万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 元/件.
元/件.
(1)将该产品的利润y(万元)表示为促销费用x(万元)的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log2(![]() a).
a).
(Ⅰ)当a=1,解不等式f(x)>1;
(Ⅱ)设a>0,若对任意t∈(﹣1,0],函数f(x)在区间[t,t+1]上的最大值与最小值的和不大于log26,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com