
分析 如图所示,考虑⊙Cn,⊙Cn+1外切.可得|CnCn+1|=rn+rn+1,设⊙Cn,⊙Cn+1分别与直线OB相切于点Bn和Bn+1,作Cn+1Dn⊥BnCn于点Dn.则|DnCn|=rn-rn+1,在Rt△CnDnCn+1中,sin$\frac{θ}{2}$=$\frac{{D}_{n}{C}_{n}}{{C}_{n}{C}_{n+1}}$=$\frac{{r}_{n}-{r}_{n+1}}{{r}_{n}+{r}_{n+1}}$,可得$\frac{{r}_{n+1}}{{r}_{n}}$=$\frac{1-sin\frac{θ}{2}}{1+sin\frac{θ}{2}}$,则q=$\frac{{S}_{n+1}}{{S}_{n}}$=$(\frac{{r}_{n+1}}{{r}_{n}})^{2}$=$(\frac{1-sin\frac{θ}{2}}{1+sin\frac{θ}{2}})^{2}$,因此{rn}与{Sn}均是无穷递减的等比数列.利用$\underset{lim}{n→∞}$(S1+S2+…+Sn)=$\frac{{S}_{1}}{1-q}$=$\frac{π(1+sin\frac{θ}{2})^{2}}{4sin\frac{θ}{2}}$=$\frac{9π}{8}$,化简为$2si{n}^{2}\frac{θ}{2}$-5$sin\frac{θ}{2}$+2=0,θ为锐角,解出即可.
解答 解:如图所示,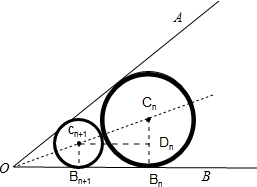
考虑⊙Cn,⊙Cn+1外切.
∵三点O,Cn,Cn+1共线,
∴|CnCn+1|=rn+rn+1,
设⊙Cn,⊙Cn+1分别与直线OB相切于点Bn和Bn+1,作Cn+1Dn⊥BnCn于点Dn.
则|DnCn|=rn-rn+1,在Rt△CnDnCn+1中,sin$\frac{θ}{2}$=$\frac{{D}_{n}{C}_{n}}{{C}_{n}{C}_{n+1}}$=$\frac{{r}_{n}-{r}_{n+1}}{{r}_{n}+{r}_{n+1}}$,
∴$\frac{{r}_{n+1}}{{r}_{n}}$=$\frac{1-sin\frac{θ}{2}}{1+sin\frac{θ}{2}}$,
则q=$\frac{{S}_{n+1}}{{S}_{n}}$=$(\frac{{r}_{n+1}}{{r}_{n}})^{2}$=$(\frac{1-sin\frac{θ}{2}}{1+sin\frac{θ}{2}})^{2}$
∴$0<\frac{{S}_{n+1}}{{S}_{n}}<1$;$0<\frac{{r}_{n+1}}{{r}_{n}}<1$,
∴{rn}与{Sn}均是无穷递减的等比数列.
∴$\underset{lim}{n→∞}$(S1+S2+…+Sn)=$\frac{{S}_{1}}{1-q}$=$\frac{π(1+sin\frac{θ}{2})^{2}}{4sin\frac{θ}{2}}$=$\frac{9π}{8}$,
化简为$2si{n}^{2}\frac{θ}{2}$-5$sin\frac{θ}{2}$+2=0,$sin\frac{θ}{2}$≤1,解得$sin\frac{θ}{2}$=$\frac{1}{2}$,
∵θ为锐角,∴$\frac{θ}{2}$=$\frac{π}{6}$,解得θ=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了无穷递减的等比数列的极限性质、圆的面积、两圆外切的性质、三角函数求值,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | y=2x+1 | B. | y=2x+3 | C. | y=x+2 | D. | y=3x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{e^2}{4}$,+∞) | B. | ($\frac{{{e^{\;}}}}{2}$,+∞) | C. | (1,$\frac{e^2}{4}$) | D. | (1,$\frac{{{e^{\;}}}}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -200 | B. | -100 | C. | 200 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.
过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com