
分析 画出函数f(x)=min{x${\;}^{\frac{1}{3}}$,2x-2,1-3x}的图象可判断①;根据f(x)+f($\frac{1}{x}$)=0,可判断②;画出函数函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{2}(x∈A)}\\{-2x+2(x∈B)}\end{array}\right.$的图象,数形结合,可判断③;根据复合函数的单调性和对数函数的图象和性质,可判断④;讨论满足函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-a(x<1)}\\{4(x-a)(x-2a),(x≥1)}\end{array}\right.$恰有2个零点的实数a的取值范围,可判断⑤.
解答 解:函数f(x)=min{x${\;}^{\frac{1}{3}}$,2x-2,1-3x}的图象如下图所示: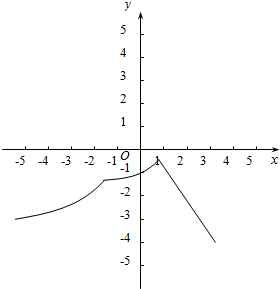
由图可得,函数存在最大值,故①正确;
函数f(x)=$\frac{1+{x}^{2}}{1-{x}^{2}}$(x≠±1),则f(x)+f($\frac{1}{x}$)=0,
故f(2)+f(3)+f(4)+f($\frac{1}{2}$)+f($\frac{1}{3}$)+f($\frac{1}{4}$)=0,故②正确;
设集合A=[0,$\frac{1}{2}$),B=[$\frac{1}{2}$,1],函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{2}(x∈A)}\\{-2x+2(x∈B)}\end{array}\right.$的图象如下图所示:
若f[f(x0)]∈A,则f(x0)∈($\frac{3}{4}$,1],
又由x0∈A,故x∈($\frac{1}{4}$,$\frac{1}{2}$),故③正确;
函数y=f(x)为函数y=$(\frac{1}{2})^{x}$的反函数,则f(x)=${log}_{\frac{1}{2}}x$;
若y=f(-x2-ax+1)在x∈(2,3)上单调递增,
则x∈(2,3)时,t=-x2-ax+1为减函数,且t>0恒成立,
故$\left\{\begin{array}{l}-\frac{a}{2}≤2\\-9-3a+1≥0\end{array}\right.$,解得:a∈[-4,-$\frac{8}{3}$],故④错误;
设h(x)=2x-a,g(x)=4(x-a)(x-2a),
若在x<1时,h(x)=2x-a与x轴有一个交点,
所以a>0,并且当x=1时,h(1)=2-a>0,所以0<a<2,
而函数g(x)=4(x-a)(x-2a)有一个交点,所以2a≥1,且a<1,
所以$\frac{1}{2}$≤a<1,
若函数h(x)=2x-a在x<1时,与x轴没有交点,
则函数g(x)=4(x-a)(x-2a)有两个交点,
当a≤0时,h(x)与x轴无交点,g(x)无交点,所以不满足题意(舍去),
当h(1)=2-a≤0时,即a≥2时,g(x)的两个交点满足x1=a,x2=2a,都是满足题意的,
综上所述a的取值范围是[$\frac{1}{2}$,1)∪[2,+∞),故⑤正确;
故正确的命题有:①②③⑤,
故答案为:①②③⑤
点评 本题考查的知识点是函数的图象和性质,函数的最值,函数求值,分段函数的应用,反函数,函数的单调性,函数的零点,是函数图象和性质的综合应用,综合性强,属于难题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | {x|x≤-$\sqrt{2}$或x≥1} | C. | {x|x≤1或a≥2} | D. | {x|x≤2或x≥3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com