练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．设复数z=$\frac{2+i}{（1+i）^{2}}$（i为虚数单位），则z的共轭复数的虚部是1．

    分析 直接利用复数代数形式的乘除运算化简，再求出$\overline{z}$得答案．

    解答 解：由z=$\frac{2+i}{（1+i）^{2}}$=$\frac{2+i}{2i}=\frac{（2+i）（-i）}{-2{i}^{2}}=\frac{1}{2}-i$，
    ∴$\overline{z}=\frac{1}{2}+i$．
    ∴z的共轭复数的虚部是1．
    故答案为：1．

    点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．下面四个推理，不属于演绎推理的是（　　）
    A．因为函数y=sinx（x∈R）的值域为[-1，1]，2x-1∈R，所以y=sin（2x-1）（x∈R）的值域也为[-1，1]
    B．昆虫都是6条腿，竹节虫是昆虫，所以竹节虫有6条腿
    C．在平面中，对于三条不同的直线a，b，c，若a∥b，b∥c则a∥c，将此结论放到空间中也是如此
    D．如果一个人在墙上写字的位置与他的视线平行，那么，墙上字迹离地的高度大约是他的身高，凶手在墙上写字的位置与他的视线平行，福尔摩斯量得墙壁上的字迹距地面六尺多，于是，他得出了凶手身高六尺多的结论

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

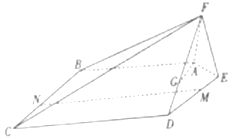    8．如图，在五棱锥F-ABCDE中，平面AEF⊥平面ABCDE，AF=EF=1，AB=DE=2，BC=CD=3，且∠AFE=∠ABC=∠BCD=∠CDE=90°．
    （1）已知点G在线段FD上，确定G的位置，使得AG∥平面BCF；
    （2）点M，N分别在线段DE，BC上，若沿直线MN将四边形MNCD向上翻折，D与F恰好重合，求三棱锥A-BMF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知等比数列{an}的前n项和为Sn，公比q=$\frac{1}{2}$，a8=1，则S8=255．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知当x＞0时，不等式x2-mx+4＞0恒成立，则实数m的取值范围是（-∞，4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知a＞0，x，y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤4}\\{y≥a（x-4）}\end{array}\right.$，若z=2x+y的最小值是-1，则a=（　　）
    A．$\frac{1}{4}$B．$\frac{1}{2}$C．2D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．（1）求定积分${∫}_{-2}^{1}$|x2-2|dx的值；
    （2）若复数z1=a+2i（a∈R），z2=3-4i，且$\frac{{z}_{1}}{{z}_{2}}$为纯虚数，求|z1|

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．若椭圆$\frac{x^2}{{{m^2}+1}}+{y^2}=1$的离心率为$\frac{{\sqrt{3}}}{2}$，则它的长半轴长为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．在平面直角坐标系xOy中，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且右焦点F到左准线的距离为6$\sqrt{2}$．
    （1）求椭圆C的标准方程；
    （2）设A为椭圆C的左顶点，P为椭圆C上位于x轴上方的点，直线PA交y轴于点M，过点F作MF的垂线，交y轴于点N．
    （i）当直线PA的斜率为$\frac{1}{2}$时，求△MFN的外接圆的方程；
    （ii）设直线AN交椭圆C于另一点Q，求△PAQ的面积的最大值．

    查看答案和解析>>

    同步练习册答案