解:(1)在△MF
1F
2中,MF
12+MF
22-2MF
1•MF
2cos∠F
1MF
2=4c
2即:(MF
1+MF
2)
2-3MF
1•MF
2=4c
2即:4a
2-3MF
1•MF
2=4c
2,则3MF
1•MF
2=4a
2-4c
2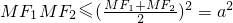
,当且仅当MF
1=MF
2=a时,取等号
∴4a
2-4c
2≤3a
2,即a
2≤4c
2∴
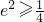
即
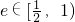
(2)令OP=m,则m∈[b,a]
又PF
1+PF
2=2a
在三角形O与三角形O中分别用余弦定理表示出PF
12与PF
22两式相加可得:PF
12+PF
22=2m
2+2c
2则(PF
1-PF
2)
2=4(m
2+c
2-a
2)
∴
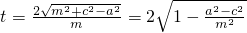
∵m∈[b,a],∴
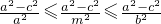
即
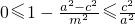
,
∴t的取值范围是
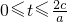
.
分析:(1)在△MF
1F
2中,根据余弦定理得4a
2-3MF
1•MF
2=4c
2,则3MF
1•MF
2=4a
2-4c
2结合基本不等式即可求得,当且仅当MF
1=MF
2=a时,a
2≤4c
2从而求椭圆的离心率e的取值范围.
(2)令OP=m,结合椭圆的定义由余弦定理可得(PF
1-PF
2)
2=4(m
2+c
2-a
2),得到
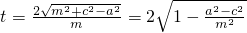
最后利用放缩法即可求得t的取值范围是.
点评:本小题主要考查椭圆的简单性质、基本不等式等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

 的两个焦点F1(-c,0)、F2(c,0),M是椭圆C上一点,且满足
的两个焦点F1(-c,0)、F2(c,0),M是椭圆C上一点,且满足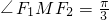 .
.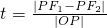 的取值范围.
的取值范围.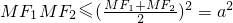 ,当且仅当MF1=MF2=a时,取等号
,当且仅当MF1=MF2=a时,取等号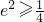 即
即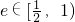
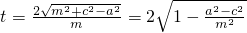
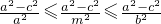
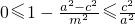 ,
,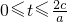 .
.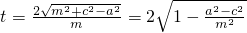 最后利用放缩法即可求得t的取值范围是.
最后利用放缩法即可求得t的取值范围是.

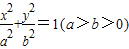 的两个焦点为F1(-1,0),F2(1,0),点
的两个焦点为F1(-1,0),F2(1,0),点 在椭圆C上.
在椭圆C上.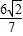 ,求直线l的方程.
,求直线l的方程. 的两个焦点为F1(-1,0),F2(1,0),点
的两个焦点为F1(-1,0),F2(1,0),点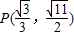 在椭圆C上.
在椭圆C上. ,求直线l的方程.
,求直线l的方程.