求下列数列的前n项和Sn:
(1)a,2a2,3a3,…,nan,…;
(2)1×3,2×4,3×5,4×6,…
【答案】
分析:(1)分a=1,a≠1两种情况求解,当a=1时为等差数列易求;当a≠1时利用错位相减法即可求得;
(2)其通项为a
n=n(n+2)=n
2+2n,根据通项对数列各项进行分组求和,再运用公式即可求得;
解答:解:(1)当a=1时,S
n=1+2+3+…+n=
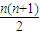
;
当a≠1时,S
n=a+2a
2+3a
3+…+na
n,①
aS
n=a
2+2a
3+3a
4+…+na
n+1,②
①-②得,(1-a)S
n=a+a
2+a
3+a
4+…+a
n-na
n+1=
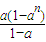
-na
n+1,
所以S
n=
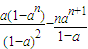
.
所以当a=1时,S
n=
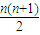
;当a≠1时,S
n=
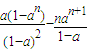
.
(2)数列通项a
n=n(n+2)=n
2+2n,
则S
n=1×3+2×4+3×5+4×6+…+n(n+2)
=(1
2+2×1)+(2
2+2×2)+(3
2+2×3)+(4
2+2×4)+…+(n
2+2n)
=(1
2+2
2+3
2+…+n
2)+2(1+2+3+4+…+n)
=
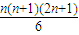
+2×
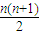
=n
2+n.
点评:本题主要考查等差、等比数列的求和公式,考查错位相减法、分组求和法,属中档题,熟记相关方法及有关公式是解决该类问题的基础.

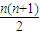 ;
;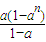 -nan+1,
-nan+1,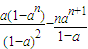 .
.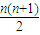 ;当a≠1时,Sn=
;当a≠1时,Sn=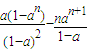 .
.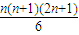 +2×
+2×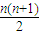 =n2+n.
=n2+n.

 名校课堂系列答案
名校课堂系列答案