解:(1)∵f(x)=x
2+ax的最小值不小于-1,∴
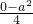
≥-1,即 a
2≤4,-2≤a≤2.
再由f(

)
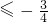
可得

-

≤-

,a≥2.
综上可得,a=2,f(x)=x
2+2x.
(2)二次 函数F(x)=f(x)-kx+1=x
2+2x-kx+1 的图象开口向上,对称轴为 x=
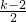
,又 x∈[-2,2],.
当
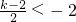
,即 k<-2,时,函数F(x)在[-2,2]上是增函数,故当x=-2时,函数F(X)取得最小值为 g(k)=2k+1.
当
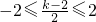
,即-2≤k≤6时,当x=
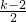
时,函数F(X)取得最小值为 g(k)=-

k
2+k.
当
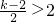
,即 k>6时,函数F(x)在[-2,2]上是减函数,故当x=2时,函数F(X)取得最小值为 g(k)=9-2k.
综上可得,
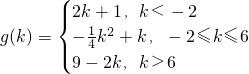
.
分析:(1)由f(x)=x
2+ax的最小值不小于-1 求得-2≤a≤2.再由f(

)
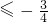
可得 a≥2,由此求得a的值,从而得到函数f(x)的解析式.
(2)二次 函数F(x)=f(x)-kx+1=x
2+2x-kx+1 的图象开口向上,对称轴为 x=
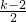
,分对称轴在区间的左边、在区间上、在区间的右边三种情况,分别求出 g(k),从而得出结论.
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属于中档题.

 )
)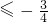 .
.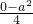 ≥-1,即 a2≤4,-2≤a≤2.
≥-1,即 a2≤4,-2≤a≤2. )
)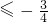 可得
可得  -
- ≤-
≤- ,a≥2.
,a≥2.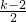 ,又 x∈[-2,2],.
,又 x∈[-2,2],.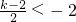 ,即 k<-2,时,函数F(x)在[-2,2]上是增函数,故当x=-2时,函数F(X)取得最小值为 g(k)=2k+1.
,即 k<-2,时,函数F(x)在[-2,2]上是增函数,故当x=-2时,函数F(X)取得最小值为 g(k)=2k+1.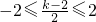 ,即-2≤k≤6时,当x=
,即-2≤k≤6时,当x=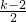 时,函数F(X)取得最小值为 g(k)=-
时,函数F(X)取得最小值为 g(k)=- k2+k.
k2+k.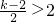 ,即 k>6时,函数F(x)在[-2,2]上是减函数,故当x=2时,函数F(X)取得最小值为 g(k)=9-2k.
,即 k>6时,函数F(x)在[-2,2]上是减函数,故当x=2时,函数F(X)取得最小值为 g(k)=9-2k.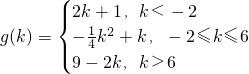 .
. )
)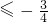 可得 a≥2,由此求得a的值,从而得到函数f(x)的解析式.
可得 a≥2,由此求得a的值,从而得到函数f(x)的解析式.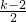 ,分对称轴在区间的左边、在区间上、在区间的右边三种情况,分别求出 g(k),从而得出结论.
,分对称轴在区间的左边、在区间上、在区间的右边三种情况,分别求出 g(k),从而得出结论.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<