
 sinxcosx+2cos2x-t.
sinxcosx+2cos2x-t. ]上有解,求t的取值范围;
]上有解,求t的取值范围; sin2x,cos2x=
sin2x,cos2x= (1+cos2x)
(1+cos2x) sinxcosx+2cos2x-t=
sinxcosx+2cos2x-t= sin2x+cos2x+1-t
sin2x+cos2x+1-t +cos2xsin
+cos2xsin )+1-t=2sin(2x+
)+1-t=2sin(2x+ )+1-t
)+1-t ]时,2x+
]时,2x+ ∈[
∈[ ,
, ],可得-
],可得- ≤sin(2x+
≤sin(2x+ )≤1
)≤1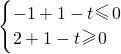 ,解之得0≤t≤3;
,解之得0≤t≤3; )+1-t=2sin(2x+
)+1-t=2sin(2x+ )-2
)-2 )-2=-1,sin(2A+
)-2=-1,sin(2A+ )=
)=

 =(b+c)2-3bc
=(b+c)2-3bc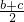 )2=1
)2=1 )+1-t,结合正弦函数图象与性质,根据f(x)=0在x∈[0,
)+1-t,结合正弦函数图象与性质,根据f(x)=0在x∈[0, ]上有解建立关于t的不等式组,解之即可得到实数t的取值范围;
]上有解建立关于t的不等式组,解之即可得到实数t的取值范围; )-2=-1,结合A是三角形的内角解出A=
)-2=-1,结合A是三角形的内角解出A= .结合余弦定理得a2关于b、c的式子,最后利用基本不等式求最值,可得当且仅当b=c=1时,a的最小值为1.
.结合余弦定理得a2关于b、c的式子,最后利用基本不等式求最值,可得当且仅当b=c=1时,a的最小值为1. ]上有解时t的取值范围,并依此求三角形的边长的最小值,着重考查了三角恒等变换、三角函数的图象与性质、余弦定理和基本不等式等知识,属于中档题.
]上有解时t的取值范围,并依此求三角形的边长的最小值,着重考查了三角恒等变换、三角函数的图象与性质、余弦定理和基本不等式等知识,属于中档题. 

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com