练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】椭圆的右顶点和上顶点分别为,斜率为的直线与椭圆交于两点(点在第一象限).

    (Ⅰ)求证：直线的斜率之和为定值；

    (Ⅱ)求四边形面积的取值范围.

    【答案】(Ⅰ)见解析；(Ⅱ).

    【解析】

    (Ⅰ)设直线方程为：代入并整理得：,利用韦达定理与斜率公式可得而，化简即可得结果；(Ⅱ)设的左顶点和下顶点分别为、,则直线、、为互相平行的直线,所以、两点到直线的距离等于两平行线、间的距离.，利用弦长公式以及三角形面积公式可得，从而可得结果.

    (Ⅰ)设直线方程为：代入椭圆并整理得：

    设,则.

    从而

    所以直线 、的斜率之和为定值0.

    (Ⅱ)设的左顶点和下顶点分别为、,则直线、、为互相平行的直线,所以、两点到直线的距离等于两平行线、间的距离.

    ,又点在第一象限,

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】幻彩摩天轮位于中山市西区兴中广场C段4层高的建筑之上，与中山市第一家四星级酒店——富华酒店隔河相望，其外观是参考世界最高的摩天轮新加坡“飞行者”的设计，轮体上有36个吊舱，共可同时承载288人从高空俯瞰岐江一河两岸的美景．幻彩摩天轮直径为83m，每20min转一圈，最高点离地108m，摩天轮上的点P的起始位置在最低点处．已知在时刻t（min）时P距离地面的高度，（其中），

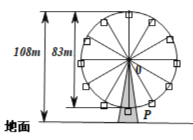
    （1）求的函数解析式．

    （2）当离地面m以上时，可以俯瞰富华酒店顶楼，求转一圈中有多少时间可以俯瞰富华酒店顶楼？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知△中，∠=90°，，且=1，=2，△绕旋转至，使点与点之间的距离=．

    （1）求证：⊥平面；

    （2）求二面角的大小；

    （3）求异面直线与所成的角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝||，实数m，n满足0＜m＜n，且f(m)＝f(n)，若f(x)在[m2，n]上的最大值为2，则＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出，将冰雪这个冷项目迅速炒“热”．北京某综合大学计划在一年级开设冰球课程，为了解学生对冰球运动的兴趣，随机从该校一年级学生中抽取了100人进行调查，其中女生中对冰球运动有兴趣的占，而男生有10人表示对冰球运动没有兴趣额．

    （1）完成列联表，并回答能否有的把握认为“对冰球是否有兴趣与性别有关”？

    有兴趣

    没兴趣

    合计

    男

    55

    女

    合计

    （2）已知在被调查的女生中有5名数学系的学生，其中3名对冰球有兴趣，现在从这5名学生中随机抽取3人，求至少有2人对冰球有兴趣的概率．

    附表：

    0.150

    0.100

    0.050

    0.025

    0.010

    2.072

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，.

    （1）若，求函数在上的最小值；

    （2）求函数的极值点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知不交于同一点的三条直线：4x＋y－4＝0，：mx＋y＝0，：x－my－4＝0.

    (1)当这三条直线不能围成三角形时，求实数m的值；

    (2)当与，都垂直时，求两垂足间的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】20名学生某次数学考试成绩(单位：分)的频率分布直方图如下：

    (1)求频率直方图中a的值；

    (2)分别求出成绩落在[50,60)与[60,70)中的学生人数；

    (3)从成绩在[50,70)的学生中人选2人，求这2人的成绩都在[60,70)中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某糕点房推出一类新品蛋糕，该蛋糕的成本价为4元，售价为8元．受保质期的影响，当天没有销售完的部分只能销毁．经过长期的调研，统计了一下该新品的日需求量．现将近期一个月（30天）的需求量展示如下：

    日需求量x（个）

    20

    30

    40

    50

    天数

    5

    10

    10

    5

    （1）从这30天中任取两天，求两天的日需求量均为40个的概率．

    （2）以上表中的频率作为概率，列出日需求量的分布列，并求该月的日需求量的期望．

    （3）根据（2）中的分布列求得当该糕点房一天制作35个该类蛋糕时，对应的利润的期望值为；现有员工建议扩大生产一天45个，求利用利润的期望值判断此建议该不该被采纳．

    查看答案和解析>>

    同步练习册答案