
分析 化简椭圆方程为标准方程,求出a,b利用离心率求出m,然后求解椭圆长轴、焦点坐标、顶点坐标.
解答 解:原方程变形为$\frac{x^2}{m}+\frac{y^2}{{\frac{m}{m+3}}}=1$,因为m>0,所以长轴为x轴,即$a=\sqrt{m}$,$b=\sqrt{\frac{m}{m+3}}$,c=$\sqrt{\frac{{m}^{2}+2m}{m+3}}$,
所以$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,将c和a代入解得m=1,椭圆的标准方程为${x^2}+\frac{y^2}{{\frac{1}{4}}}=1$,
所以长轴长为2,短轴长为1,焦点为$({\frac{{\sqrt{3}}}{2},0})$,$({-\frac{{\sqrt{3}}}{2},0})$,
顶点坐标分别为(1,0)、(-1,0)、$({0,\frac{1}{2}})$、$({0,-\frac{1}{2}})$.
点评 本题考查椭圆方程的求法,椭圆的简单性质的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
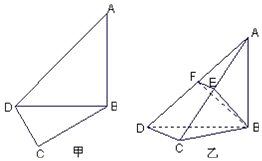 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
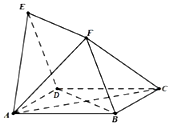 如图,平面四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图,平面四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 60° | C. | 30° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|4x<2x+1} | B. | $\left\{{y\left|{y=\sqrt{x-1}}\right.}\right\}$ | ||
| C. | $\{y|y=sinx,-\frac{π}{3}≤x≤\frac{π}{6}\}$ | D. | $\left\{{(x,y)\left|{y={{log}_2}(-{x^2}+2x+1)}\right.}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(4)<f(7) | B. | f(4)>f(7) | C. | f(5)>f(7) | D. | f(5)<f(7) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
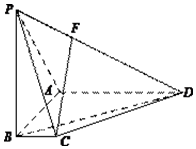 如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.
如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com