
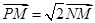 .
.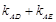 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由. (2)
(2) 
 ,涉及两个动点问题,往往是通过相关点法求对应轨迹方程,此时也要设已知轨迹上的动点
,涉及两个动点问题,往往是通过相关点法求对应轨迹方程,此时也要设已知轨迹上的动点 ,则
,则 ,二是列出动点满足的条件
,二是列出动点满足的条件 ,用未知动点坐标表示已知动点坐标,即
,用未知动点坐标表示已知动点坐标,即 ,三是代入化简,
,三是代入化简, ,四是去杂,主要看是否等价转化,本题无限制条件, (2)定值问题,往往是坐标化简问题,即多参数消元问题. 利用斜率公式,直线方程化简
,四是去杂,主要看是否等价转化,本题无限制条件, (2)定值问题,往往是坐标化简问题,即多参数消元问题. 利用斜率公式,直线方程化简
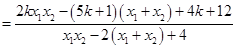 ,再利用韦达定理
,再利用韦达定理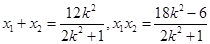 代入化简得常数
代入化简得常数 ,从过程看是四元变为二元,再变为一元,最后变为常数,一个逐步消元的运算过程,有运算量,无思维量.
,从过程看是四元变为二元,再变为一元,最后变为常数,一个逐步消元的运算过程,有运算量,无思维量. ,
, ,则
,则 ,
, ,
,
 ,得
,得 ,
, 3分
3分 在圆
在圆 上,则有
上,则有 ,即
,即 .
. 点
点 的轨迹
的轨迹 的方程为
的方程为 . 6分
. 6分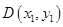 ,
, ,过点
,过点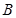 的直线
的直线 的方程为
的方程为 ,
, 消去
消去 得:
得: 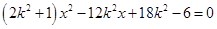 ,其中
,其中
 ; 8分
; 8分
 10分
10分

 是定值
是定值 . 13分
. 13分

科目:高中数学 来源:不详 题型:解答题
 =
=
 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 =1,过点M(0,1)的直线l交椭圆于A,B两点,O是坐标原点,点P满足
=1,过点M(0,1)的直线l交椭圆于A,B两点,O是坐标原点,点P满足 =
= (
( +
+ ),当l绕点M旋转时,动点P的轨迹方程为 .
),当l绕点M旋转时,动点P的轨迹方程为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 +
+ =1(a>b>0)的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM∥x轴,
=1(a>b>0)的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM∥x轴, ·
· =9,若点P的坐标为(0,t),则t的取值范围是( )
=9,若点P的坐标为(0,t),则t的取值范围是( )
| A.0<t<3 | B.0<t≤3 |
C.0<t< | D.0<t≤ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 =1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为
=1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为 .
. ⊥
⊥ ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
.过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com