
| 2 | k-1 |
| 2 |
| k-1 |
| 3an |
| 3an-1 |
| 2 |
| k-1 |
| ak |
| k |
| ak-1 |
| k-1 |
| ak |
| k |
| ak-1 |
| k-1 |


科目:高中数学 来源: 题型:
| (n-2)•r•(r-1) |
| 2 |
| (n-2)•r•(r-1) |
| 2 |

查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市等八校高三2月联合调研考试理科数学试卷 题型:解答题
由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列” ,将构图边数增加到
,将构图边数增加到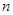 可得到“
可得到“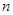 边形数列”,记它的第
边形数列”,记它的第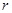 项为
项为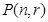 ,
,
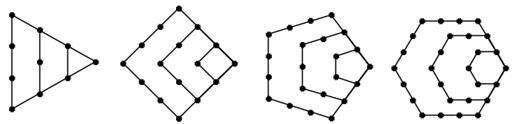
1,3,6,10 1,4,9,16 1,5,12,22 1,6,15,28
(1)
求使得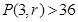 的最小
的最小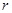 的取值;
的取值;
(2)
试推导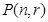 关于
关于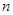 、
、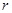 的解析式;
的解析式;
( 3) 是否存在这样的“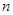 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省稳派教育高三数学强化训练试卷1(理科)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com