Question

【题目】新高考3+3最大的特点就是取消文理科，除语文、数学、外语之外，从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目．某研究机构为了了解学生对全理（选择物理、化学、生物）的选择是否与性别有关决定从某学校高一年级的650名学生中随机抽取男生、女生各25人进行模拟选科经统计，选择全理的人数比不选全理的人数多10人

（1）请完成下面的2×2列联表；

	选择全理	不选择全理	合计
男生		5
女生
合计

（2）估计有多大把握认为选择全理与性别有关，并说明理由．

附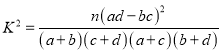：，其中n＝a+b+c+d

P（K2≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.076	3.841	5.024	6.635	7.879	10.828

Answer 1

【答案】（1）见解析（2）有99.5%的把握认为选择全理与性别有关

【解析】

（1）根据男、女生人数以及选择全理的人数比不选全理的人数多10人填写表格；

（2）计算的值，然后与表格所给数据作比对，从而得出有多大把握认为选择全理与性别有关.

（1）依题意可得列联表：

	选择全理	不选择全理	合计
男生	20	5	25
女生	10	15	25
合计	30	20	50

（2），

∴有99.5%的把握认为选择全理与性别有关．