
ЁОЬтФПЁПЩш![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЮЊШЁздФГзмЬхЕФбљБОЃЌЦфЫуЪѕЦНОљжЕГЦЮЊбљБООљжЕЃЌвЛАугУ
ЮЊШЁздФГзмЬхЕФбљБОЃЌЦфЫуЪѕЦНОљжЕГЦЮЊбљБООљжЕЃЌвЛАугУ![]() БэЪОЃЌМД
БэЪОЃЌМД![]() ЃЌдкЗжзщбљБОГЁКЯЃЌбљБООљжЕЕФНќЫЦЙЋЪНЮЊ
ЃЌдкЗжзщбљБОГЁКЯЃЌбљБООљжЕЕФНќЫЦЙЋЪНЮЊ![]() ЃЌЦфжаkЮЊзщЪ§ЃЌ
ЃЌЦфжаkЮЊзщЪ§ЃЌ![]() ЮЊЕкiзщЕФзщжажЕЃЌ
ЮЊЕкiзщЕФзщжажЕЃЌ![]() ЮЊЕкiзщЕФЦЕЪ§.ФГЕЅЮЛЪеМЏЕН20УћЧрФъЕФФГЬьгщРжжЇГіЗбгУЪ§ОнЃК
ЮЊЕкiзщЕФЦЕЪ§.ФГЕЅЮЛЪеМЏЕН20УћЧрФъЕФФГЬьгщРжжЇГіЗбгУЪ§ОнЃК
79 84 84 88 92 93 94 97 98 99
100 101 101 102 102 108 110 113 118 125
ШєНЋЗжЮЊЮхзщЃЌЕквЛзщЮЊ![]() ЃЌИљОнЗжзщбљБОМЦЫубљБООљжЕЮЊЃЈ ЃЉ
ЃЌИљОнЗжзщбљБОМЦЫубљБООљжЕЮЊЃЈ ЃЉ
A.99.4B.143.16C.100D.11.96
 УЯНЈЦНДэЬтБОЯЕСаД№АИ
УЯНЈЦНДэЬтБОЯЕСаД№АИ ГЌФмбЇЕфгІгУЬтЬтПЈЯЕСаД№АИ
ГЌФмбЇЕфгІгУЬтЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊМЏКЯ![]() ЃЌШєЖдгкШЮвт
ЃЌШєЖдгкШЮвт![]() ЃЌДцдк
ЃЌДцдк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ГЩСЂЃЌдђГЦМЏКЯ
ГЩСЂЃЌдђГЦМЏКЯ![]() ЪЧЁА
ЪЧЁА![]() МЏКЯЁБ.ИјГіЯТСа5ИіМЏКЯЃК
МЏКЯЁБ.ИјГіЯТСа5ИіМЏКЯЃК
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛ
ЃЛ
Ђм![]() ЃЛЂн
ЃЛЂн![]() .
.
ЦфжаЪЧЁА![]() МЏКЯЁБЕФЫљгаађКХЪЧЃЈ ЃЉ
МЏКЯЁБЕФЫљгаађКХЪЧЃЈ ЃЉ
A.ЂкЂлB.ЂйЂмЂнC.ЂкЂлЂнD.ЂйЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкКЏЪ§![]() ЃЌШєДцдкЧјМф
ЃЌШєДцдкЧјМф![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌдђГЦКЏЪ§
ЃЌдђГЦКЏЪ§![]() ЮЊЁАПЩЕШгђКЏЪ§ЁБЃЌЧјМф
ЮЊЁАПЩЕШгђКЏЪ§ЁБЃЌЧјМф![]() ЮЊКЏЪ§
ЮЊКЏЪ§![]() ЕФвЛИіЁАПЩЕШгђЧјМфЁБЃЎИјГіЯТСа4ИіКЏЪ§ЃК
ЕФвЛИіЁАПЩЕШгђЧјМфЁБЃЎИјГіЯТСа4ИіКЏЪ§ЃК
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛ Ђл
ЃЛ Ђл![]() ЃЛ Ђм
ЃЛ Ђм![]() ЃЎ
ЃЎ
ЦфжаДцдкЮЈвЛЁАПЩЕШгђЧјМфЁБЕФЁАПЩЕШгђКЏЪ§ЁБЮЊЃЈ ЃЉ
ЃЈAЃЉЂйЂкЂл ЃЈBЃЉЂкЂл ЃЈCЃЉЂйЂл ЃЈDЃЉЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌТњзу
ЃЌТњзу![]() .Щш
.Щш![]() ЮЊ
ЮЊ![]() ЩЯШЮвЛЕу,Й§
ЩЯШЮвЛЕу,Й§![]() зї
зї![]() ЕФЧаЯп,ЦфаБТЪ
ЕФЧаЯп,ЦфаБТЪ![]() Тњзу
Тњзу![]()
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЪ§Са![]() Тњзу
Тњзу![]() .Щш
.Щш![]() ЮЊе§ГЃЪ§.
ЮЊе§ГЃЪ§.
ЂйЧѓ![]() ЃЛ
ЃЛ
ЂкШєВЛЕШЪН![]() ЖдШЮвтЕФ
ЖдШЮвтЕФ![]() КуГЩСЂЃЌдђЪЕЪ§
КуГЩСЂЃЌдђЪЕЪ§![]() ЪЧЗёДцдкзюДѓжЕ?ШєДцдк,ЧыЧѓГіетИіжЕЃЛШєВЛДцдк,ЧыЫЕУїРэгЩ.
ЪЧЗёДцдкзюДѓжЕ?ШєДцдк,ЧыЧѓГіетИіжЕЃЛШєВЛДцдк,ЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкЦНУцжБНЧзјБъЯЕЃЌНЋЧњЯп![]() ЩЯЕФУПвЛИіЕуЕФКсзјБъБЃГжВЛБфЃЌзнзјБъЫѕЖЬЮЊдРДЕФ
ЩЯЕФУПвЛИіЕуЕФКсзјБъБЃГжВЛБфЃЌзнзјБъЫѕЖЬЮЊдРДЕФ![]() ЃЌЕУЕНЧњЯп
ЃЌЕУЕНЧњЯп![]() ЃЌвдзјБъдЕу
ЃЌвдзјБъдЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ ![]() жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌ
жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌ ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЧѓЧњЯп![]() ЕФВЮЪ§ЗНГЬЃЛ
ЕФВЮЪ§ЗНГЬЃЛ
ЃЈЂђЃЉЙ§дЕу![]() ЧвЙигк
ЧвЙигк![]() жсЖдГЦЕФСНЬѕжБЯп
жсЖдГЦЕФСНЬѕжБЯп![]() гы
гы![]() ЗжБ№НЛЧњЯп
ЗжБ№НЛЧњЯп![]() гк
гк![]() ЁЂ
ЁЂ![]() КЭ
КЭ![]() ЁЂ
ЁЂ![]() ЃЌЧвЕу
ЃЌЧвЕу![]() дкЕквЛЯѓЯоЃЌЕБЫФБпаЮ
дкЕквЛЯѓЯоЃЌЕБЫФБпаЮ![]() ЕФжмГЄзюДѓЪБЃЌЧѓжБЯп
ЕФжмГЄзюДѓЪБЃЌЧѓжБЯп![]() ЕФЦеЭЈЗНГЬЃЎ
ЕФЦеЭЈЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВCЃК![]() ЃЈ
ЃЈ![]() ЃЉОЙ§Еу
ЃЉОЙ§Еу![]() ЃЌРыаФТЪЮЊ
ЃЌРыаФТЪЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊЭждВЕФзѓЁЂгвНЙЕу.
ЗжБ№ЮЊЭждВЕФзѓЁЂгвНЙЕу.
ЃЈ1ЃЉЧѓЭждВCЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉШєЕу![]() ЃЈ
ЃЈ![]() ЃЉдкЭждВCЩЯЃЌЧѓжЄЃЛжБЯп
ЃЉдкЭждВCЩЯЃЌЧѓжЄЃЛжБЯп![]() гыжБЯп
гыжБЯп![]() ЙигкжБЯпlЃК
ЙигкжБЯпlЃК![]() ЖдГЦ.
ЖдГЦ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌНЧAЃЌBЃЌCЫљЖдЕФБпЗжБ№ЮЊaЃЌbЃЌcЃЌЧвТњзуbcosAЉ![]() asinBЃН0ЃЎ
asinBЃН0ЃЎ
ЃЈ1ЃЉЧѓAЃЛ
ЃЈ2ЃЉвбжЊaЃН2![]() ЃЌBЃН
ЃЌBЃН![]() ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ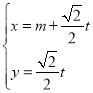 ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌЧвЧњЯп
ЃЌЧвЧњЯп![]() ЕФзѓНЙЕу
ЕФзѓНЙЕу![]() дкжБЯп
дкжБЯп![]() ЩЯ.
ЩЯ.
ЃЈЂёЃЉЧѓ![]() ЕФМЋзјБъЗНГЬКЭЧњЯп
ЕФМЋзјБъЗНГЬКЭЧњЯп![]() ЕФВЮЪ§ЗНГЬЃЛ
ЕФВЮЪ§ЗНГЬЃЛ
ЃЈЂђЃЉЧѓЧњЯп![]() ЕФФкНгОиаЮЕФжмГЄЕФзюДѓжЕ.
ЕФФкНгОиаЮЕФжмГЄЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPЉABCDжаADЁЮBCЃЌDAЁЭABЃЌADЃН2ЃЌABЃНBCЃН1ЃЌCD![]() ЃЌЕуEЮЊPDжаЕу.
ЃЌЕуEЮЊPDжаЕу.
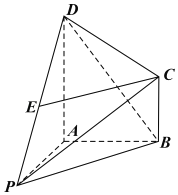
ЃЈ1ЃЉЧѓжЄЃКCEЁЮЦНУцPABЃЛ
ЃЈ2ЃЉШєPAЃН2ЃЌPDЃН2![]() ЃЌЁЯPAB
ЃЌЁЯPAB![]() ЃЌЧѓЦНУцPBDгыЦНУцECDЫљГЩШёЖўУцНЧЕФгрЯвжЕ.
ЃЌЧѓЦНУцPBDгыЦНУцECDЫљГЩШёЖўУцНЧЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com