
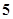 张假钞的
张假钞的 张百元钞票中任意抽取
张百元钞票中任意抽取 张,将其中一张在验钞机上检验发现是假钞,问这
张,将其中一张在验钞机上检验发现是假钞,问这 张都是假钞的概率是( )
张都是假钞的概率是( )A. | B. | C. | D. |
科目:高中数学 来源:不详 题型:单选题
| A.100 90 | B.100 180 | C.200 180 | D.200 360 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验. 的概率分布列和期望.
的概率分布列和期望. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 和
和 ,据统计,通过两条路径所用的时间互不影响,所用时间落在个时间段内的频率如下表:
,据统计,通过两条路径所用的时间互不影响,所用时间落在个时间段内的频率如下表:
| 时间(分钟) | 10 20 20 | 20 30 30 | 30 40 40 | 40 50 50 | 50 60 60 |
 的频率 的频率 |  |  |  |  |  |
 的频率 的频率 | 0 |  |  |  |  |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 的期望
的期望 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com