
| 生产量x(单位:吨) | 50 | 100 | 130 | 180 | 200 | 250 | 300 |
| 生产总成本y(单位:万元) | 2750 | 2000 | 1750 | 1800 | 2050 | 2750 | 4050 |
分析 (1)由所给数据,函数先减后增,对称轴是x=150,故最恰当的函数描述y与x的变化关系是②,通过表中前两组数据,求出y与x的函数解析式;
(2)生产每吨的平均成本$\frac{y}{x}$=$\frac{x}{10}$+$\frac{4000}{x}$-30,利用基本不等式,即可得出结论;
(3)L=16x-$\frac{{x}^{2}}{10}$+30x-4000=-$\frac{{x}^{2}}{10}$+46x-4000=-$\frac{1}{10}$(x-230)2+1290,即可求解.
解答 解:(1)由所给数据,函数先减后增,对称轴是x=150,故最恰当的函数描述y与x的变化关系是②,其函数解析式为y=$\frac{{x}^{2}}{10}$-30x+4000(50≤x≤300);
(2)$\frac{y}{x}$=$\frac{x}{10}$+$\frac{4000}{x}$-30≥2$\sqrt{\frac{x}{10}•\frac{4000}{x}}$-30=10,当且仅当x=200吨时,生产每吨的平均成本最低,每吨的最低成本是10万元/吨;
(3)L=16x-$\frac{{x}^{2}}{10}$+30x-4000=-$\frac{{x}^{2}}{10}$+46x-4000=-$\frac{1}{10}$(x-230)2+1290,
∴x=230时,全年的利润最大,全年的最大利润为1290万元.
点评 本题考查利用数学知识解决实际问题,考查基本不等式的运用,考查配方法,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
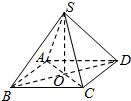 如图,已知四棱锥S-ABCD的侧棱与底面边长都是2,且底面ABCD是正方形,则侧棱与底面所成的角( )
如图,已知四棱锥S-ABCD的侧棱与底面边长都是2,且底面ABCD是正方形,则侧棱与底面所成的角( )| A. | 75° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
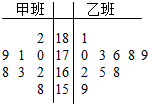 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图示,根据茎叶图解答下列问题;
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图示,根据茎叶图解答下列问题;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
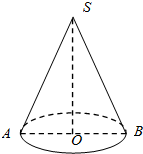 如图,在圆锥SO中,其母线长为2,底面半径为$\frac{1}{2}$,一只虫子从底面圆周上一点A出发沿圆锥表面爬行一周后又回到A点,则这只虫子所爬过的最短路程是2$\sqrt{2}$.
如图,在圆锥SO中,其母线长为2,底面半径为$\frac{1}{2}$,一只虫子从底面圆周上一点A出发沿圆锥表面爬行一周后又回到A点,则这只虫子所爬过的最短路程是2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
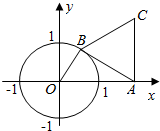 如图的平面直角坐标系中,O为坐标原点,点B在单位圆上,A(2,0),∠AOB=θ,△ABC为等边三角形.
如图的平面直角坐标系中,O为坐标原点,点B在单位圆上,A(2,0),∠AOB=θ,△ABC为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com