
分析 由“e度和谐函数”,得到对任意的x∈[$\frac{1}{e}$,e],都有|f(x)-g(x)|≤1,化简整理得m-e≤lnx+$\frac{1}{x}$≤m+e,
令h(x)=lnx+$\frac{1}{x}$($\frac{1}{e}$≤x≤e),求出h(x)的最值,只要m-1不大于最小值,且m+1不小于最大值即可.
解答 解:∵函数f(x)=lnx与g(x)=$\frac{mx-1}{x}$在[$\frac{1}{e}$,e],
∴对任意的x∈[$\frac{1}{e}$,e],都有|f(x)-g(x)|≤1,
即有|lnx-$\frac{mx-1}{x}$|≤1,即m-1≤lnx+$\frac{1}{x}$≤m+1,
令h(x)=lnx+$\frac{1}{x}$($\frac{1}{e}$≤x≤e),h′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$,
x>1时,h′(x)>0,x<1时,h′(x)<0,
x=1时,h(x)取极小值1,也为最小值,
故h(x)在[$\frac{1}{e}$,e]上的最小值是1,最大值是e-1.
∴m-1≤1且m+1≥e-1,
∴e-2≤m≤2.
故答案为:[e-2,2].
点评 本题考查新定义及运用,考查不等式的恒成立问题,转化为求函数的最值,注意运用导数求解,是一道中档题.


科目:高中数学 来源: 题型:选择题
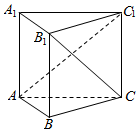 三棱柱ABC-A1B1C1中,△ABC是等边三角形,AA1⊥底面ABC,AB=2,AA1=$\sqrt{2}$,则异面直线AC1与B1C所成的角的大小是( )
三棱柱ABC-A1B1C1中,△ABC是等边三角形,AA1⊥底面ABC,AB=2,AA1=$\sqrt{2}$,则异面直线AC1与B1C所成的角的大小是( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
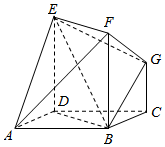 如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE,CG=$\frac{1}{2}$DE.
如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE,CG=$\frac{1}{2}$DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:
将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com