
【题目】如图,长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=m,点M是棱CD的中点.
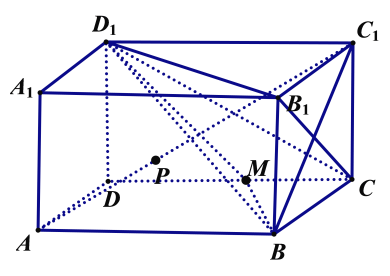
(1)求异面直线B1C与AC1所成的角的大小;
(2)是否存在实数m,使得直线AC1与平面BMD1垂直?说明理由;
(3)设P是线段AC1上的一点(不含端点),满足![]() λ,求λ的值,使得三棱锥B1﹣CD1C1与三棱锥B1﹣CD1P的体积相等.
λ,求λ的值,使得三棱锥B1﹣CD1C1与三棱锥B1﹣CD1P的体积相等.
【答案】(1)90° (2)存在,m![]() ,理由见解析 (3)λ
,理由见解析 (3)λ![]()
【解析】
(1)根据题意只需证明![]() 平面
平面![]() ,即可得到B1C⊥AC1,从而可得答案.
,即可得到B1C⊥AC1,从而可得答案.
(2)存在实数m![]() ,使得直线AC1与平面BMD1垂直.只需证明BM⊥AC1,AC1⊥D1M,即可得到直线AC1⊥平面BMD1;
,使得直线AC1与平面BMD1垂直.只需证明BM⊥AC1,AC1⊥D1M,即可得到直线AC1⊥平面BMD1;
(3)计算![]() ,
,![]() ,设AC1 与平面B1CD1 的斜足为O,则AO=2OC1,则P为AO的中点,从而可得答案.
,设AC1 与平面B1CD1 的斜足为O,则AO=2OC1,则P为AO的中点,从而可得答案.
(1)连接BC1,如图所示:

由四边形BCC1B1为正方形,可得B1C⊥BC1,
又ABCD﹣A1B1C1D1为长方体,可得AB⊥B1C,而AB∩BC1=B,
∴B1C⊥平面ABC1,而AC1平面ABC1,∴B1C⊥AC1,
即异面直线B1C与AC1所成的角的大小为90°;
(2)存在实数m![]() ,使得直线AC1与平面BMD1垂直.
,使得直线AC1与平面BMD1垂直.
事实上,当m![]() 时,CM
时,CM![]() ,
,
∵BC=1,∴![]() ,则Rt△ABC∽Rt△BCM,
,则Rt△ABC∽Rt△BCM,
则∠CAB=∠MBC,
∵∠CAB+∠ACB=90°,∴∠MBC+∠ACB=90°,即AC⊥BM,
又CC1⊥BM,AC∩CC1=C,∴BM⊥平面ACC1,则BM⊥AC1,
同理可证AC1⊥D1M,
又D1M∩BM=M,∴直线AC1⊥平面BMD1;
(3)∵![]() ,
,
![]() ,
,
设AC1 与面B1CD1 的斜足为O,则AO=2OC1,
∴在线段AC1上取一点P,要使三棱锥B1﹣CD1C1与三棱锥B1﹣CD1P的体积相等,
则P为AO的中点,即![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
(1)在频率分布直方图中,中位数左边和右边的直方图的面积相等.
(2)如果一组数中每个数减去同一个非零常数,则这一组数的平均数改变,方差不改变.
(3)一个样本的方差s2=![]() [(x
[(x![]() 一3)2+(X
一3)2+(X![]() —3)2+ +(X
—3)2+ +(X![]() 一3)2],则这组数据总和等于60.
一3)2],则这组数据总和等于60.
(4)数据![]() 的方差为
的方差为![]() ,则数据
,则数据![]() 的方差为
的方差为![]() .
.
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与平面
与平面![]() 相交但不垂直,则下列说法中正确的是( )
相交但不垂直,则下列说法中正确的是( )
A.在平面![]() 内没有直线与直线
内没有直线与直线![]() 垂直;
垂直;
B.在平面![]() 内有且只有一条直线与直线
内有且只有一条直线与直线![]() 垂直;
垂直;
C.在平面![]() 内有无数条直线与直线
内有无数条直线与直线![]() 垂直;
垂直;
D.在平面![]() 内存在两条相交直线与直线
内存在两条相交直线与直线![]() 垂直.
垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
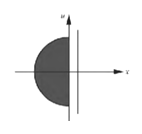
【题目】关于旋转体的体积,有如下的古尔丁(guldin)定理:“平面上一区域D绕区域外一直线(区域D的每个点在直线的同侧,含直线上)旋转一周所得的旋转体的体积,等于D的面积与D的几何中心(也称为重心)所经过的路程的乘积”.利用这一定理,可求得半圆盘 ,绕直线x
,绕直线x![]() 旋转一周所形成的空间图形的体积为_____.
旋转一周所形成的空间图形的体积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
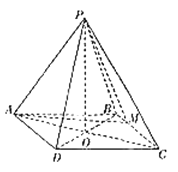
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,顶点
为菱形,顶点![]() 在底面
在底面![]() 的射影恰好是菱形
的射影恰好是菱形![]() 对角线的交点
对角线的交点![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年10月考考试中,成都外国语学校共有250名高三文科学生参加考试,数学成绩的频率分布直方图如图:
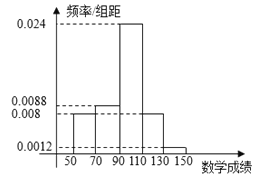
(1)如果成绩大于130的为特别优秀,这250名学生中本次考试数学成绩特别优秀的大约多少人?
(2)如果这次考试语文特别优秀的有5人,语文和数学两科都特别优秀的共有2人,从(1)中的数学成绩特别优秀的人中随机抽取2人,求选出的2人中恰有1名两科都特别优秀的概率.
(3)根据(1),(2)的数据,是否有99%以上的把握认为语文特别优秀的同学,数学也特别优秀?
①![]()
②
P( | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com