解:(I)∵数列{a
n}的前n项和S
n=2n
2+2n,
∴a
1=S
1=2+2=4,
a
n=S
n-S
n-1=(2n
2+2n)-[2(n-1)
2+2(n-1)]=4n,
当n=1时,4n=4=a
1,
∴a
n=4n.
∵数列{b
n}的前n项和T
n=2-b
n,
∴当n=1时,T
1=b
1=2-b
1,解得b
1=1.
当n>1时,T
n=2-b
n,T
n-1=2-b
n-1,
∴T
n-T
n-1=b
n=b
n-1-b
n,∴2b
n=b
n-1,
∴
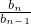
=

,
∴数列{b
n}是以首项为1,公比为

的等比数列,
∴
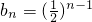
,n∈N
*.
(II)∵
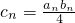
=n
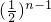
,
∴数列{c
n}的前n和:
R
n=c
1+c
2+c
3+…+c
n=1•(

)
0+2×(

)
1+3×(

)
2+…+(n-1)•(

)
n-2+n•(

)
n-1,①
∴

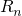
=1•(

)
1+2×(

)
2+3×(

)
3+…+(n-1)•(

)
n-1+n•(

)
n,②
①-②,得
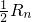
=1+

+(

)
2+(

)
3+…+(

)
n-1-n•(

)
n
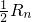
=
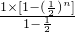
-n•(

)
n
=2-
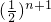
-n•(

)
n,
∴
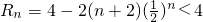
;
( III)∵c
n=a
n+(-1)
nlog
2b
n=4n+
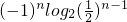
=4n+(-1)
n(1-n),
∴数列{c
n}的前2n和
R
2n=[4×1+(-1)
1(1-1)]+[4×2+(-1)
2(1-2)]+[4×3+(-1)
3(1-3)]+…+[4×2n+(-1)
2n(1-2n)]
=4(1+2+3+…+2n)+[0-1+2-3+…+(2n-2)-(2n-1)]
=4×

-n
=8n
2+3n.
∴R
2n=8n
2+3n.
分析:(I)由数列{a
n}的前n项和S
n=2n
2+2n,知a
1=S
1=2+2=4,a
n=S
n-S
n-1=(2n
2+2n)-[2(n-1)
2+2(n-1)]=4n,由此能求出a
n.由数列{b
n}的前n项和T
n=2-b
n,知当n=1时,T
1=b
1=2-b
1,解得b
1=1.当n>1时,T
n=2-b
n,T
n-1=2-b
n-1,故T
n-T
n-1=b
n=b
n-1-b
n,2b
n=b
n-1,由此能求出b
n.
(II)由
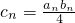
=n
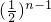
,知数列{c
n}的前n和:R
n=c
1+c
2+c
3+…+c
n=1•(

)
0+2×(

)
1+3×(

)
2+…+(n-1)•(

)
n-2+n•(

)
n-1,由错位相减法能够证明
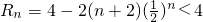
;
( III)由c
n=a
n+(-1)
nlog
2b
n=4n+
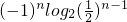
=4n+(-1)
n(1-n),能求出数列{c
n}的前2n和.
点评:本题考查数列的通项公式的求法,考查数列前n项和公式的求法,解题时要认真审题,注意迭代法、错位相减法、分组求和法的灵活运用.

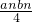 ,求证数列{cn}的前n和Rn<4;
,求证数列{cn}的前n和Rn<4;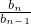 =
= ,
, 的等比数列,
的等比数列,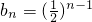 ,n∈N*.
,n∈N*.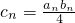 =n
=n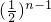 ,
, )0+2×(
)0+2×( )1+3×(
)1+3×( )2+…+(n-1)•(
)2+…+(n-1)•( )n-2+n•(
)n-2+n•( )n-1,①
)n-1,①
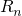 =1•(
=1•( )1+2×(
)1+2×( )2+3×(
)2+3×( )3+…+(n-1)•(
)3+…+(n-1)•( )n-1+n•(
)n-1+n•( )n,②
)n,②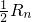 =1+
=1+ +(
+( )2+(
)2+( )3+…+(
)3+…+( )n-1-n•(
)n-1-n•( )n
)n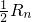 =
=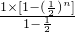 -n•(
-n•( )n
)n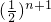 -n•(
-n•( )n,
)n,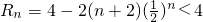 ;
;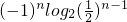
 -n
-n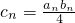 =n
=n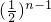 ,知数列{cn}的前n和:Rn=c1+c2+c3+…+cn=1•(
,知数列{cn}的前n和:Rn=c1+c2+c3+…+cn=1•( )0+2×(
)0+2×( )1+3×(
)1+3×( )2+…+(n-1)•(
)2+…+(n-1)•( )n-2+n•(
)n-2+n•( )n-1,由错位相减法能够证明
)n-1,由错位相减法能够证明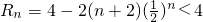 ;
;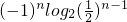 =4n+(-1)n(1-n),能求出数列{cn}的前2n和.
=4n+(-1)n(1-n),能求出数列{cn}的前2n和.

 备战中考寒假系列答案
备战中考寒假系列答案