
【题目】已知某种药物在血液中以每小时![]() 的比例衰减,现给某病人静脉注射了该药物2500mg,设经过x个小时后,药物在病人血液中的量为ymg.
的比例衰减,现给某病人静脉注射了该药物2500mg,设经过x个小时后,药物在病人血液中的量为ymg.
![]() 与x的关系式为______;
与x的关系式为______;
![]() 当该药物在病人血液中的量保持在1500mg以上,才有疗效;而低于500mg,病人就有危险,要使病人没有危险,再次注射该药物的时间不能超过______小时
当该药物在病人血液中的量保持在1500mg以上,才有疗效;而低于500mg,病人就有危险,要使病人没有危险,再次注射该药物的时间不能超过______小时![]() 精确到
精确到![]() .
.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
科目:高中数学 来源: 题型:
【题目】某宾馆有![]() 间标准相同的客房,客房的定价将影响入住率.经调查分析,得出每间客房的定价与每天的入住率的大致关系如下表:
间标准相同的客房,客房的定价将影响入住率.经调查分析,得出每间客房的定价与每天的入住率的大致关系如下表:
每间客房的定价 | 220元 | 200元 | 180元 | 160元 |
每天的入住率 |
|
|
|
|
对于每间客房,若有客住,则成本为80元;若空闲,则成本为40元.要使此宾馆每天的住房利润最高,则每间客房的定价大致应为( )
A. 220元 B. 200元 C. 180元 D. 160元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的![]() 件产品作为样本,称出它们的重量(单位:克),重量的分组区间为
件产品作为样本,称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() ,…,
,…,![]() ,由此得到样本的频率分布方图,如图所示.
,由此得到样本的频率分布方图,如图所示.
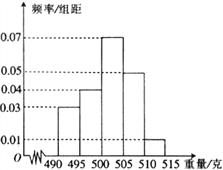
(1)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为取到重量超过
为取到重量超过![]() 克的产品件数,求
克的产品件数,求![]() 的概率;
的概率;
(2)从上述![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为取到重量超过
为取到重量超过![]() 克的产品件数,求
克的产品件数,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地,目前德国汉堡,美国波士顿等申办城市因市民担心赛事费用超支而相继退出,某机构为调查我国公民对申办奥运会的态度,选了100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | _______ | _______ | 80 |
年龄大于50岁 | 10 | _______ | _______ |
合计 | _______ | 70 | 100 |
(1)根据已知数据,把表格填写完整;
(2)是否有95%的把握认为年龄与支持申办奥运有关?
附表:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.814 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)= ![]() +lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣
+lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣ ![]() ﹣lnx(m∈R). (Ⅰ)求θ的值;
﹣lnx(m∈R). (Ⅰ)求θ的值;
(Ⅱ)若f(x)﹣g(x)在[1,+∞)上为单调函数,求m的取值范围;
(Ⅲ)设h(x)= ![]() ,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com