练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    有一段“三段论”推理是这样的：“对于可导函数，如果，那么是函数 的极值点；因为函数在处的导数值，所以是函数的极值点.”以上推理中(　　)
    A．大前提错误B．小前提错误C．推理形式错误D．结论正确
    A

    试题分析：大前提是错误的，因为对于可导函数，当，不一定是函数 的极值点，如本题中的函数，（当且仅当时，），所以函数在上单调递增，该函数没有极值点，故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

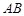    学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽为2米,，与沟沿垂直的平面与沟的交线是一段抛物线，抛物线的顶点为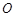，对称轴与地面垂直，沟深2米，沟中水深1米．
    （1）求水面宽；
    （2）如图1所示形状的几何体称为柱体，已知柱体的体积为底面积乘以高，求沟中的水有多少立方米？


    （3）现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟，使沟的底面与地面平行，沟深不变，两腰分别与抛物线相切（如图2），问改挖后的沟底宽为多少米时，所挖的土最少？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （2013•浙江）已知a∈R，函数f（x）=x3﹣3x2+3ax﹣3a+3．
    （1）求曲线y=f（x）在点（1，f（1））处的切线方程；
    （2）当x∈[0，2]时，求|f（x）|的最大值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数，.
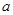    （1）求的取值范围，使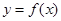在闭区间上是单调函数；
    （2）当时，函数的最大值是关于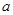的函数.求；
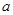    （3）求实数的取值范围，使得对任意的，恒有成立.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知函数的定义域为，当时，，且对任意的，等式成立，若数列满足，且则的值为(     )
    A．4016B．4017C．4018D．4019

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    定义max{s1，s2，…，sn}表示实数s1，s2，…，sn中的最大者．设A＝(a1，a2，a3)，B＝，记A?B＝max{a1b1，a2b2，a3b3}．设A＝(x－1，x＋1,1)，B＝，若A?B＝x－1，则x的取值范围为(　　)
    A．[1－，1]
    B．[1,1＋]
    C．[1－，1]
    D．[1,1＋]

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图，在△ABC中，∠C=90°,CA=CB=1,为△ABC内一点，过点P分别引三边的平行线，与各边围成以P为顶点的三个三角形（图中阴影部分），则这三个三角形的面积和的最小值为（  ）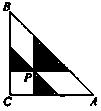
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

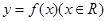    若函数满足且时，，函数分别在两相邻对称轴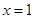与处取得最值1与-1，则函数在区间内零点的个数为（   ）
    A．1006B．1007 C．1008D．1010

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若的图像是中心对称图形,则_______.

    查看答案和解析>>

    同步练习册答案