一辆卡车高3米,宽2米,欲通过断面为抛物线型的隧道,已知拱口宽恰好是拱高的2倍,若拱口宽为2a米,求使卡车通过的a的最小整数值.
【答案】
分析:建立直角坐标系,如图:则由题意可得O、A、B、D的坐标,a>0.设抛物线的方程为 x
2=-2py,则把点B的坐标代入求得p的值,可得抛物线方程为 x
2=-ay.把x=1代入抛物线方程求得y=-
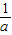
.要使卡车通过时,需 a-

≥3,由此解得a的范围,可得a的最小正整数值.
解答: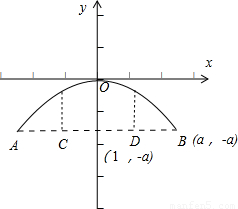
解:以拱顶为原点、抛物线的对称轴为y轴,建立直角坐标系,如图:
则由题意可得O(0,0)、A(-a,-a)、B(a,-a)、C(-1,-a)、D(1,-a),a>0.
设抛物线的方程为 x
2=-2py,则把点B的坐标代入可得p=

,
∴抛物线方程为 x
2=-ay.
把x=1代入抛物线方程可得 y=-
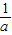
.
要使卡车通过时,需 a-

≥3,解得 a≥
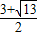
,或a≤
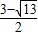
(舍去).
故a的最小正整数为4.
点评:本题主要考查抛物线的标准方程的应用,用坐标法解决几何问题,属于中档题.

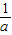 .要使卡车通过时,需 a-
.要使卡车通过时,需 a- ≥3,由此解得a的范围,可得a的最小正整数值.
≥3,由此解得a的范围,可得a的最小正整数值. 解:以拱顶为原点、抛物线的对称轴为y轴,建立直角坐标系,如图:
解:以拱顶为原点、抛物线的对称轴为y轴,建立直角坐标系,如图: ,
,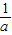 .
. ≥3,解得 a≥
≥3,解得 a≥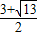 ,或a≤
,或a≤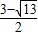 (舍去).
(舍去).
