
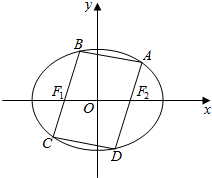
 如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.
如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.分析 (Ⅰ)通过$\left\{\begin{array}{l}x-2y=0\\ 3{x^2}+4{y^2}=12\end{array}\right.$,求出x,得到A,C两点的坐标,利用距离公式求解即可.
(Ⅱ)①当直线AD的斜率不存在时,求出三个点的坐标,然后求解平行四边形的面积.
②当直线AD的斜率存在时,设直线AD的方程为y=k(x-1),与椭圆方程联立,设点A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).利用韦达定理,连结AF1,DF1,表示出面积表达式,然后求解最值.
解答 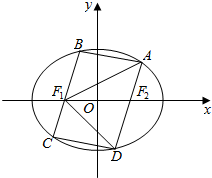 (本小题满分14分)
(本小题满分14分)
(Ⅰ)解:由$\left\{\begin{array}{l}x-2y=0\\ 3{x^2}+4{y^2}=12\end{array}\right.$,消去y可得:4x2=12,解得$x=±\sqrt{3}$,(2分)
所以A,C两点的坐标为$(\sqrt{3},\frac{{\sqrt{3}}}{2})$和$(-\sqrt{3},-\frac{{\sqrt{3}}}{2})$,(4分)
所以 $|{AC}|=\sqrt{{{(2\sqrt{3})}^2}+{{(\sqrt{3})}^2}}=\sqrt{15}$.(5分)
(Ⅱ)解:①当直线AD的斜率不存在时,
此时易得$A(1,\frac{3}{2})$,$B(-1,\frac{3}{2})$,$C(-1,-\frac{3}{2})$,$D(1,-\frac{3}{2})$,
所以平行四边形ABCD的面积为|AB|•|AD|=6.(6分)
②当直线AD的斜率存在时,设直线AD的方程为y=k(x-1),
将其代入椭圆方程,整理得(3+4k2)x2-8k2x+4k2-12=0.(8分)
设点A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).
则 ${x_1}+{x_4}=\frac{{8{k^2}}}{{3+4{k^2}}}$,${x_1}{x_4}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$.(10分)
连结AF1,DF1,
则平行四边形ABCD的面积$S=2{S_{△A{F_1}D}}=\;|{F_1}{F_2}||{y_1}-{y_4}|\;=2|{y_1}-{y_4}|$.(11分)
又 ${({y_1}-{y_4})^2}={k^2}{({x_1}-{x_4})^2}={k^2}[{({x_1}+{x_4})^2}-4{x_1}{x_4}]$=$9×\frac{{16{k^2}({k^2}+1)}}{{{{(3+4{k^2})}^2}}}$.(13分)
又(3+4k2)2-16k2(k2+1)=9+8k2,
所以 $S=6\sqrt{\frac{16{k}^{2}({k}^{2}+1)}{{(3+4{k}^{2})}^{2}}}=6\sqrt{1-\frac{9+8{k}^{2}}{{(3+4{k}^{2})}^{2}}}<6$.
综上,平行四边形ABCD面积的最大值是6.(14分)
点评 本题考查椭圆的方程的求法,直线与椭圆的综合应用,考查分析问题解决问题的能力,转化思想的应用.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2+2$\sqrt{5}$+$\sqrt{14}$ | B. | 16+2$\sqrt{14}$ | C. | 8+2$\sqrt{14}$ | D. | 8+$\sqrt{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos(2x+$\frac{π}{3}$) | B. | y=cos(2x-$\frac{π}{3}$) | C. | y=cos($\frac{1}{2}$x+$\frac{π}{3}$) | D. | y=cos($\frac{1}{2}$x-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(b)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(a)<f(c) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com