
【题目】已知函数![]() 在
在![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求a,b的值;
(2)若对任意![]() ,都有
,都有![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由切线方程求出![]() 及
及![]() ,由函数解析式求出函数在
,由函数解析式求出函数在![]() 处的函数值及导数值,即可求出
处的函数值及导数值,即可求出![]() 的值;(2)将问题转化为对任意
的值;(2)将问题转化为对任意![]() ,都有
,都有![]() 恒成立,构造函数,利用函数的单调性求解.
恒成立,构造函数,利用函数的单调性求解.
(1)由函数![]() 在
在![]() 处的切线方程是
处的切线方程是![]() 可知,
可知,![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以![]() 得
得![]()
(2)由(1)知![]() .
.
若对任意![]() ,都有
,都有![]() 恒成立,
恒成立,
则对任意![]() ,都有
,都有![]() 恒成立,
恒成立,
化简得![]() .
.
令![]() ,所以对任意
,所以对任意![]() ,都有
,都有![]() .
.
易知![]() ,
,
令![]() ,
,
则![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,即当
,即当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,符合题意.
,符合题意.
当![]() 时,易知
时,易知![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() .
.
若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,即当
,即当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,符合题意.
,符合题意.
若![]() ,令
,令![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,于是有
,于是有![]() ,
,
即![]() ,
,
得![]() .
.
因为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
即![]() 在
在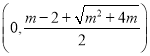 上是减函数,
上是减函数,
所以当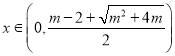 时,
时,![]() ,
,
即![]() ,所以
,所以![]() 在
在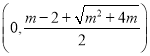 上是减函数,
上是减函数,
所以当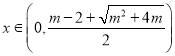 时,
时,![]() ,与
,与![]() 矛盾,不符合题意.
矛盾,不符合题意.
故实数![]() 的取值范围是
的取值范围是![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
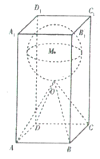
【题目】在日常生活中,石子是我们经常见到的材料,比如在各种建筑工地或者建材市场上常常能看到堆积如山的石子,它的主要成分是碳酸钙.某雕刻师计划在底面边长为2m、高为4m的正四棱柱形的石料![]() 中,雕出一个四棱锥
中,雕出一个四棱锥![]() 和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中
和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中![]() ,石料的密度
,石料的密度![]() ,质量
,质量![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ABB1A1是边长为2的菱形,且CA=CB1.
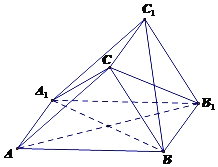
(1)证明:面CBA1⊥面CB1A;
(2)若∠BAA1=60°,A1C=BC=BA1,求点C到平面A1BC1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
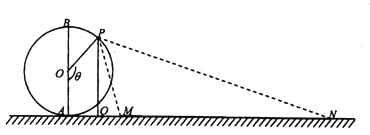
【题目】如图,摩天轮的半径![]() 为
为![]() ,它的最低点
,它的最低点![]() 距地面的高度忽略不计.地上有一长度为
距地面的高度忽略不计.地上有一长度为![]() 的景观带
的景观带![]() ,它与摩天轮在同一竖直平面内,且
,它与摩天轮在同一竖直平面内,且![]() .点
.点![]() 从最低点
从最低点![]() 处逆时针方向转动到最高点
处逆时针方向转动到最高点![]() 处,记
处,记![]() .
.
(1)当![]() 时,求点
时,求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)试确定![]() 的值,使得
的值,使得![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的棱长均为6,其内有
的棱长均为6,其内有![]() 个小球,球
个小球,球![]() 与三棱锥
与三棱锥![]() 的四个面都相切,球
的四个面都相切,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切,如此类推,…,球
都相切,如此类推,…,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切(
都相切(![]() ,且
,且![]() ),则球
),则球![]() 的体积等于__________,球
的体积等于__________,球![]() 的表面积等于__________.
的表面积等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选题)下列说法正确的是( )
A.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均减少2.3个单位
平均减少2.3个单位
B.两个具有线性相关关系的变量,当相关指数![]() 的值越接近于0,则这两个变量的相关性就越强
的值越接近于0,则这两个变量的相关性就越强
C.若两个变量的相关指数![]() ,则说明预报变量的差异有88%是由解释变量引起的
,则说明预报变量的差异有88%是由解释变量引起的
D.在回归直线方程![]() 中,相对于样本点
中,相对于样本点![]() 的残差为
的残差为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东京夏季奥运会推迟至2021年7月23日至8月8日举行,此次奥运会将设置4![]() 100米男女混泳接力赛这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳
100米男女混泳接力赛这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场.若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者蛙泳,剩下2名运动员四种泳姿都可以承担,则中国队参赛的安排共有( )
自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场.若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者蛙泳,剩下2名运动员四种泳姿都可以承担,则中国队参赛的安排共有( )
A.144种B.8种C.24种D.12种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com