
【题目】已知数列![]() 的通项公式为
的通项公式为![]() ,数列
,数列![]() 的通项公式为
的通项公式为![]() ,设
,设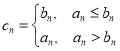 ,若在数列
,若在数列![]() 中,
中,![]() 对任意
对任意![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是_________.
的取值范围是_________.
科目:高中数学 来源: 题型:
【题目】男运动员![]() 名,女运动员
名,女运动员![]() 名,其中男女队长各
名,其中男女队长各![]() 人,从中选
人,从中选![]() 人外出比赛,分别求出下列情形有多少种选派方法?(以数字作答)
人外出比赛,分别求出下列情形有多少种选派方法?(以数字作答)
![]() 男
男![]() 名,女
名,女![]() 名;
名;
![]() 队长至少有
队长至少有![]() 人参加;
人参加;
![]() 至少
至少![]() 名女运动员;
名女运动员;
![]() 既要有队长,又要有女运动员.
既要有队长,又要有女运动员.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人各射击一次,击中目标的概率分别是![]() 和
和![]() . 假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
. 假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击. 问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按下列要求分配6本不同的书,各有多少种不同的分配方式?
(1)分成三份,1份1本,1份2本,1份3本;
(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;
(3)平均分成三份,每份2本;
(4)平均分配给甲、乙、丙三人,每人2本;
(5)分成三份,1份4本,另外两份每份1本;
(6)甲、乙、丙三人中,一人得4本,另外两人每人得1本;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在前三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同排课顺序共有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
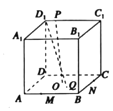
【题目】在正方体![]() 中边长AB为2,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,Q为正方形ABCD内一点,M,N分别为AB,BC上靠近A和C的三等分点,若线段
中边长AB为2,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,Q为正方形ABCD内一点,M,N分别为AB,BC上靠近A和C的三等分点,若线段![]() 与OP相交且互相平分,则点Q的轨迹与线段MN形成的封闭图形的面积为____.
与OP相交且互相平分,则点Q的轨迹与线段MN形成的封闭图形的面积为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com