已知函数 f(x)的导数.f′(x)=3x2-3ax,f(0)=b,a,b为实数,1<a<2.
(1) 若f(x)在区间_[-1,1]_上的最小值、最大值分别为-2、1,求a,b的值;
(2) 在(1)的条件下,求曲线在点P(2,1)处的切线方程.
【答案】
分析:(1)由已知的f(x)的导函数的解析式及f(0)=b,表示出f(x)的解析式,令导函数等于0,求出x的值,根据a的范围,检验得到满足题意的x的值,在闭区间[-1,1]上,根据x的值分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性分别求出函数f(x)在闭区间[-1,1]上的最大值和最小值,又最小值、最大值分别为-2、1,即可求出a与b的值;
(2)由(1)求出的a与b代入得到f(x)的解析式及导函数的解析式,把点P的横坐标代入导函数中即可求出切线的下课,根据切点和求出的斜率写出切线l的方程即可.
解答:解:(1)由已知f′(x)=3x
2-3ax,f(0)=b,
得f(x)=x
3-

ax
2+b,
由f′(x)=0即3x
2-3ax=3x(x-a),解得x=0或x=a,
∵x∈[-1,1],1<a<2,
∴当x∈[-1,0)时,f′(x)>0,f(x)单调增;当x∈(0,1]时,f′(x)<0,f(x)单调减,
∴f(x)在区间[-1,1]上的最大值为f(0)=b,∴b=1,
又f(1)=1-

a+1,f(-1)=-1-

a+1=-

a,∴f(-1)<f(1)
由题意得最小值为f(-1)=-2,即-

a=-2,解得a=

.
故a=

,b=1为所求;
(2)由(1)得f(x)=x
3-2x
2+1,f′(x)=3x
2-4x,
点P(2,1)在曲线f(x)上,
当切点为P(2,1)时,切线l的斜率k=f′(x)
|x=2=4,
∴切线l的方程为y-1=4(x-2),即4x-y-7=0.
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数求闭区间上函数的最值,是一道中档题.

 ax2+b,
ax2+b, a+1,f(-1)=-1-
a+1,f(-1)=-1- a+1=-
a+1=- a,∴f(-1)<f(1)
a,∴f(-1)<f(1) a=-2,解得a=
a=-2,解得a= .
. ,b=1为所求;
,b=1为所求;

 已知函数f(x)的定义域为[-1,5],部分对应值如下表.
已知函数f(x)的定义域为[-1,5],部分对应值如下表.
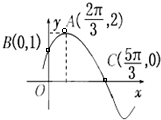
 已知函数f(x)的定义域为[-3,+∞),部分函数值如表所示,其导函数的图象如图所示,若正数a,b满足f(2a+b)<1,则
已知函数f(x)的定义域为[-3,+∞),部分函数值如表所示,其导函数的图象如图所示,若正数a,b满足f(2a+b)<1,则