
【题目】正方体![]() 的棱长为1,
的棱长为1,![]() 分别为
分别为![]() 的中点.则( )
的中点.则( )

A.直线![]() 与直线
与直线![]() 垂直B.直线
垂直B.直线![]() 与平面
与平面![]() 平行
平行
C.平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() D.点
D.点![]() 和点
和点![]() 到平面
到平面![]() 的距离相等
的距离相等
【答案】BC
【解析】
利用向量法判断异面直线所成角;利用面面平行证明线面平行;作出正方体的截面为等腰梯形,求其面积即可;利用等体积法处理点到平面的距离.
对选项A:(方法一)以![]() 点为坐标原点,
点为坐标原点,![]() 、
、![]() 、
、![]() 所在的直线分别为
所在的直线分别为![]() 、
、![]() 、
、![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .从而
.从而![]() ,
,![]() ,从而
,从而![]() ,所以
,所以![]() 与直线
与直线![]() 不垂直,选项A错误;
不垂直,选项A错误;
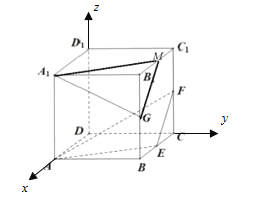
(方法二)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() 为直线
为直线![]() 在平面
在平面![]() 内的射影,
内的射影,![]() 与
与![]() 不垂直,从而
不垂直,从而![]() 与
与![]() 也不垂直,选项A错误;
也不垂直,选项A错误;
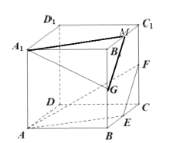
取![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() ,
,![]() ,易证
,易证![]() ,从而
,从而![]() ,选项B正确;
,选项B正确;
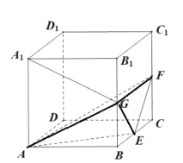
对于选项C,连接![]() ,
,![]() ,易知四边形
,易知四边形![]() 为平面
为平面![]() 截正方体所得的截面四边形(如图所示),且
截正方体所得的截面四边形(如图所示),且![]() ,
,![]() ,所以
,所以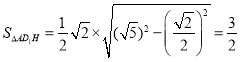 ,而
,而![]() ,从而选项C正确;
,从而选项C正确;
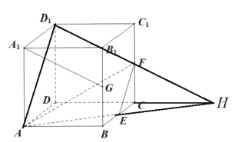
对于选项D:(方法一)由于![]() ,而
,而![]() ,而
,而![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,点
,点![]() 到平面
到平面![]() 的距离为点
的距离为点![]() 到平面
到平面![]() 的距离的二倍.从而D错误.
的距离的二倍.从而D错误.
(方法二)假设点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等,即平面
的距离相等,即平面![]() 将
将![]() 平分,则平面
平分,则平面![]() 必过
必过![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,易知
,易知![]() 不是
不是![]() 的中点,故假设不成立,从而选项D错误.
的中点,故假设不成立,从而选项D错误.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】抢“微信红包”已经成为中国百姓欢度春节时非常喜爱的一项活动.小明收集班内20名同学今年春节期间抢到红包金额![]() (元)如下(四舍五入取整数):
(元)如下(四舍五入取整数):
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
对这20个数据进行分组,各组的频数如下:

(Ⅰ)写出m,n的值,并回答这20名同学抢到的红包金额的中位数落在哪个组别;
(Ⅱ)记C组红包金额的平均数与方差分别为![]() 、
、![]() ,E组红包金额的平均数与方差分别为
,E组红包金额的平均数与方差分别为![]() 、
、![]() ,试分别比较
,试分别比较![]() 与
与![]() 、
、![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从A,E两组所有数据中任取2个,求这2个数据差的绝对值大于100的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵.将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,则阳马
,则阳马![]() 的外接球的表面积是( )
的外接球的表面积是( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/30/1913191114645504/1914064210190336/STEM/70d44ba6321c44a9bcc99e6010bf5643.png]
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限![]() 和所支出的维修费用
和所支出的维修费用![]() (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知![]() 对
对![]() 呈线性相关关系.
呈线性相关关系.
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程![]() 的回归系数
的回归系数![]() .
.
(3)估计使用年限为10年时,维修费用是多少?
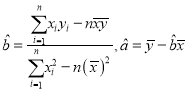
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点 ,且两个焦点的坐标分别为
,且两个焦点的坐标分别为![]() ,
, ![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 上的三个不同的点,
上的三个不同的点, ![]() 为坐标原点,且
为坐标原点,且![]() ,求证:四边形
,求证:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() 为棱
为棱![]() 中点.
中点. ![]() ,
, ![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() .
.
(II)求证: ![]() 平面
平面![]() .
.
(III)在棱![]() 的上是否存在点
的上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求此时
?如果存在,求此时![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=Acos(ωx+φ)+B的部分图象如图所示,将函数g(x)的图象保持纵坐标不变,横坐标向右平移![]() 个单位长度后得到函数f(x)的图象.求:
个单位长度后得到函数f(x)的图象.求:
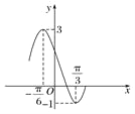
(1)函数f(x)在![]() 上的值域;
上的值域;
(2)使f(x)≥2成立的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com