分析:(1)先根据1,2,3,4,5这5个数中成公差大于1的等差数列的三个数和成公比大于1的等比数列的三个数,进而根据{a
3,a
4,a
5}∪{b
3,b
4,b
5}={1,2,3,4,5},求得a
3,a
4,a
5,b
3,b
4,b
5,进而求得等差数列的首项与公差和等比数列的首项与公比,则a
n,b
n可求得.
(2)根据(1)中的a
n,b
n可求得a
nb
n,进而用错位相减法求得数列的前n项的和.
(3)不等式
≤等价于
≤,进而整理得
≤,先看当n≥3时,根据
≤求得n的范围,进而判断出当n≥4时,{c
n}单调递增,即
{}单调递减进而看n=3,4,5,6时,求得ρ的范围,推断出恰有4个正整数n使不等式
≤成立的正整数p值为3
解答:解:(1)∵1,2,3,4,5这5个数中成公差大于1的等差数列的三个数只能是1,3,5;
成公比大于1的等比数列的三个数只能是1,2,4
而{a
3,a
4,a
5}∪{b
3,b
4,b
5}={1,2,3,4,5},
∴a
3=1,a
4=3,a
5=5,b
3=1,b
4=2,b
5=4
∴
a1=-3,d=2,b1=,q=2,
∴a
n=a
1+(n-1)d=2n-5,b
n=b
1×q
n-1=2
n-3
(2)∵a
nb
n=(2n-5)×2
n-3∴S
n=(-3)×2
-2+(-1)×2
-1+1×2
0++(2n-5)×2
n-32Sn= | | &(-3)×2-1+(-1)×20++(2n-7)×2n-3+(2n-5)×2n-2 |
| |
两式相减得-S
n=(-3)×2
-2+2×2
-1+2×2
0++2×2
n-3-(2n-5)×2
n-2
=
--1+2n-1-(2n-5)×2n-2∴
Sn=+(2n-7)×2n-2(3)不等式
≤等价于
≤即
≤,
∵p>0,∴n=1,2显然成立
当n≥3时,有
≤,
即
p≤=设
cn=,由
=>1,得n>3.5
∴当n≥4时,{c
n}单调递增,
即
{}单调递减
而当n=3时,
p≤2;
当n=4时,
p≤4;
当n=5时,
p≤3;
当n=6时,
p≤2;
∴恰有4个正整数n使不等式
≤成立的正整数p值为3
点评:本题主要考查了数列与不等式的综合.考查了学生综合分析推理的能力以及基本的运算能力.



 阅读快车系列答案
阅读快车系列答案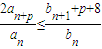 成立,求正整数p的值.
成立,求正整数p的值.