
【题目】学校高一数学考试后,对![]() 分(含
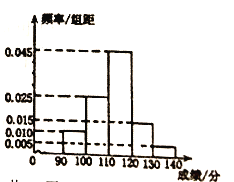
分(含![]() 分)以上的成绩进行统计,其频率分布直方图如图所示,分数在
分)以上的成绩进行统计,其频率分布直方图如图所示,分数在![]() 分的学生人数为
分的学生人数为![]() 人,
人,
(1)求这所学校分数在![]() 分的学生人数;
分的学生人数;
(2)请根据频率发布直方图估计这所学校学生分数在![]() 分的学生的平均成绩;
分的学生的平均成绩;
(3)为进“步了解学生的学习情况,按分层抽样方法从分数在![]() 分和
分和![]() 分的学生中抽出
分的学生中抽出![]() 人,从抽出的学生中选出
人,从抽出的学生中选出![]() 人分别做问卷
人分别做问卷![]() 和问卷
和问卷![]() ,求
,求![]() 分的学生做问卷
分的学生做问卷![]() ,
,![]() 分的学生做问卷
分的学生做问卷![]() 的概率.
的概率.
【答案】(1)200人;(2)113分;(3)![]() .
.
【解析】试题分析:(1)由分数在120~130分的学生人数为30人,且分数在120~130分频率为0.15,能求出分数在90~140分的学生人数.
(2)由频率分布直方图能估计这所学校学生分数在90~140分的学生的平均成绩.
(3)分数在90~100分的学生人数为20人,分数在120~130分的学生人数为30人,按照分层抽样方法抽出5人时,从分数在90~100分的学生抽出2人,记为A1,A2,从分数在![]() 分的学生抽出3人,记为B1,B2,B3,从抽取的5人中选出2人分别做问卷A和问卷B,利用列举法能求出90-100分的学生做问卷A,120-130分的学生做问卷B的概率.
分的学生抽出3人,记为B1,B2,B3,从抽取的5人中选出2人分别做问卷A和问卷B,利用列举法能求出90-100分的学生做问卷A,120-130分的学生做问卷B的概率.
试题解析:
(1)![]() 分数在
分数在![]() 分的学生人数为
分的学生人数为![]() 人,且分数在
人,且分数在![]() 分频率为
分频率为![]() ,
,![]() 分数在
分数在![]() 分的学生人数为
分的学生人数为![]() 人.
人.
(2)估计这所学校学生分数在![]() 分的学生的平均成绩为
分的学生的平均成绩为
![]() 分.
分.
(3)因为分数在![]() 分的学生人数为
分的学生人数为![]() 人,分数在
人,分数在![]() 分的学生人数为
分的学生人数为![]() 人,所以按分层抽样方法抽出
人,所以按分层抽样方法抽出![]() 人时,分数在
人时,分数在![]() 分的学生抽出
分的学生抽出![]() 人,记为
人,记为![]() ,分数在
,分数在![]() 分的学生抽出
分的学生抽出![]() 人,记为
人,记为![]() .从抽出
.从抽出![]() 人中选出
人中选出![]() 人分别做问卷
人分别做问卷![]() 和问卷
和问卷![]() ,共有
,共有![]() 种情况,分别为
种情况,分别为![]() , 设事件
, 设事件![]() “
“![]() 分的学生做问卷
分的学生做问卷![]() ,
,![]() 分的学生做问卷
分的学生做问卷![]() ”,则事件
”,则事件![]() 共有
共有![]() 种情况,分别为
种情况,分别为![]() ,
,![]() ,即事件
,即事件![]() 的概率为
的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 是
是![]() 的菱形,侧面
的菱形,侧面![]() 为正三角形,其所在平面垂直于底面
为正三角形,其所在平面垂直于底面![]() .
.
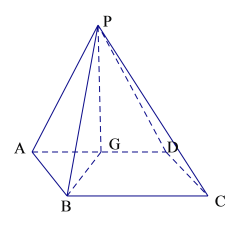
(1)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若![]() 为边
为边![]() 的中点,能否在棱
的中点,能否在棱![]() 上找到一点
上找到一点![]() ,使平面
,使平面![]() 平面
平面![]() ?并证明你的结论.
?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(![]() )若已知方程表示椭圆,则
)若已知方程表示椭圆,则![]() 的取值范围为__________.
的取值范围为__________.
(![]() )语句“
)语句“![]() ”是语句“方程
”是语句“方程![]() ”表示双曲线的(_____________).
”表示双曲线的(_____________).
A.充分不必要条件 B.必要不充分条件 C.充在条件 D.既不充分也不必要条件
(![]() )根据(
)根据(![]() )的结论,以“如果
)的结论,以“如果![]() 那么
那么![]() ”的形式写出一个正确命题,记作命题
”的形式写出一个正确命题,记作命题![]() ,则
,则
命题![]() :__________.
:__________.
(![]() )套用量词命题的格式:“
)套用量词命题的格式:“![]() ,
, ![]() ”或“
”或“![]() ,
, ![]() ”,改写(
”,改写(![]() )中命题
)中命题![]() ,
,
表述形式为:__________.
(![]() )写出(
)写出(![]() )中命题
)中命题![]() 的逆命题,记作命题
的逆命题,记作命题![]() ,则
,则
命题![]() :__________.
:__________.
(![]() )判断(
)判断(![]() )中命题
)中命题![]() 的真假,并陈述判断理由.
的真假,并陈述判断理由.
![]() 命题为__________命题,因为__________.
命题为__________命题,因为__________.
(![]() )若已知方程表示椭圆,则该椭圆两个焦点的坐标分别为__________.
)若已知方程表示椭圆,则该椭圆两个焦点的坐标分别为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
:![]() ,
,![]() :
:![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个![]() 单位长度,得到曲线
单位长度,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() 为等腰三角形,
为等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.
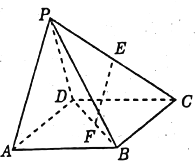
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=4sin(2x+![]() ), (x∈R)有下列命题:
), (x∈R)有下列命题:
①y=f(x)是以2π为最小正周期的周期函数;
② y=f(x)可改写为y=4cos(2x-![]() );
);
③y=f(x)的图象关于(-![]() ,0)对称;
,0)对称;
④ y=f(x)的图象关于直线x=-![]() 对称;
对称;
其中正确的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com