练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数,且函数在处的切线平行于直线.

    （1）求实数的值;

    （2）若在上存在一点,使得成立.求实数的取值范围.

    【答案】（1）（2）或.

    【解析】

    试题分析：（1）由导数几何意义得所以求导数列式得（2）本题不宜分离，因此作差构造函数，利用分类讨论法求函数最小值：由于，所以讨论与1，e的大小，分三种情况：当时,的最小值为,当时,的最小值为,当时,的最小值为，解对应不等式即得.

    试题解析：（1）的定义域为,函数在处的切线平行于直线..

    （2）若在上存在一点,使得成立,构造函数在上的最小值小于零.,

    ①当时,即时,在上单调递减,所以的最小值为,由可得,;

    ②当时,即时,在上单调递增,所以的最小值为,由可得;

    ③当时,即时,可得的最小值为,此时,不成立.综上所述:可得所求的范围是或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若函数，.

    （Ⅰ）求的单调区间和极值；

    （Ⅱ）证明：若存在零点，则在区间上仅有一个零点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，有一块矩形空地，要在这块空地上开辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB＝a(a＞2)，BC＝2，且AE＝AH＝CF＝CG，设AE＝x，绿地面积为y.

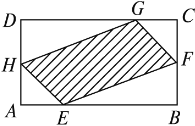
    (1)写出y关于x的函数关系式，并指出这个函数的定义域；

    (2)当AE为何值时，绿地面积y最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数,令,其中是函数的导函数.

    （1）当时,求的极值;

    （2）当时,若存在,使得恒成立,求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司采用招考方式引进人才，规定必须在，三个测试点中任意选取两个进行测试，若在这两个测试点都测试合格，则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点测试合格的概率分别为,小王在上述三个测试点测试合格的概率都是.

    （1）问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大？请说明理由;

    （2）假设小李选择测试点进行测试，小王选择测试点进行测试,记为两人在各测试点测试合格的测试点个数之和,求随机变量的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商店计划每天购进某商品若干件，商店每销售一件该商品可获利润60元，若供大于求，剩余商品全部退回，但每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利40元.

    （1）若商品一天购进该商品10件，求当天的利润（单位：元）关于当天需求量（单位：件，）的函数解析式；

    （2）商店记录了50天该商品的日需求量（单位：件，），整理得下表：

    若商店一天购进10件该商品，以50天记录的各需求量的频率作为各需求量发生的概率，求当天的利润在区间内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两同学在高考前各做了5次立定跳远测试，测得甲的成绩如下(单位：米)：2.20，2.30，2.30，2.40，2.30，若甲、乙两人的平均成绩相同，乙的成绩的方差是0.005，那么甲、乙两人成绩较稳定的是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

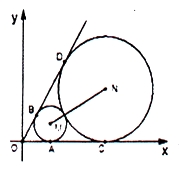
    【题目】如图，已知圆心坐标为的圆与轴及直线分别相切于、两点，另一圆与圆外切，且与轴及直线分别相切于、两点．

    （1）求圆和圆的方程；

    （2）过点作直线的平行线，求直线被圆截得的弦的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】扬州瘦西湖隧道长米，设汽车通过隧道的速度为米/秒．根据安全和车流的需要，当时，相邻两车之间的安全距离为米；当时，相邻两车之间的安全距离为米（其中是常数）．当时，，当时，．

    （1）求的值；

    （2）一列由辆汽车组成的车队匀速通过该隧道（第一辆汽车车身长为米，其余汽车车身长为米，每辆汽车速度均相同）．记从第一辆汽车车头进入隧道，至第辆汽车车尾离开隧道所用的时间为秒．

    ①将表示为的函数；

    ②要使车队通过隧道的时间不超过秒，求汽车速度的范围．

    查看答案和解析>>

    同步练习册答案