
【题目】如图,三条直线型公路![]() ,
,![]() ,
,![]() 在点
在点![]() 处交汇,其中
处交汇,其中![]() 与
与![]() 、
、![]() 与
与![]() 的夹角都为
的夹角都为![]() ,在公路
,在公路![]() 上取一点
上取一点![]() ,且
,且![]() km,过
km,过![]() 铺设一直线型的管道
铺设一直线型的管道![]() ,其中点
,其中点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上(
上(![]() ,
,![]() 足够长),设
足够长),设![]() km,
km,![]() km.
km.
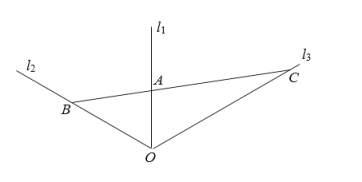
(1)求出![]() ,
,![]() 的关系式;
的关系式;
(2)试确定![]() ,
,![]() 的位置,使得公路
的位置,使得公路![]() 段与
段与![]() 段的长度之和最小.
段的长度之和最小.
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】海关对同时从![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
地区 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如表:
新能源汽车补贴标准 | |||
车辆类型 | 续驶里程R(公里) | ||
100≤R<180 | 180≤R<280 | <280 | |
纯电动乘用车 | 2.5万元/辆 | 4万元/辆 | 6万元/辆 |
某校研究性学习小组,从汽车市场上随机选取了M辆纯电动乘用车,根据其续驶里程R(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
分组 | 频数 | 频率 |
100≤R<180 | 3 | 0.3 |
180≤R<280 | 6 | x |
R≥280 | y | z |
合计 | M | 1 |
(1)求x、y、z、M的值;
(2)若从这M辆纯电动乘用车任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为X(单位:万元),求X的分布列和数学期望值E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫、精准脱贫”的号召,某贫困县在精准推进上下实功,在在精准落实上见实效现从全县扶贫对象中随机抽取![]() 人对扶贫工作的满意度进行调查,以茎叶图中记录了他们对扶贫工作满意度的分数(满分
人对扶贫工作的满意度进行调查,以茎叶图中记录了他们对扶贫工作满意度的分数(满分![]() 分)如图所示,已知图中的平均数与中位数相同.现将满意度分为“基本满意”(分数低于平均分)、“满意”(分数不低于平均分且低于
分)如图所示,已知图中的平均数与中位数相同.现将满意度分为“基本满意”(分数低于平均分)、“满意”(分数不低于平均分且低于![]() 分)和“很满意”(分数不低于
分)和“很满意”(分数不低于![]() 分)三个级别.
分)三个级别.

(1)求茎叶图中数据的平均数和![]() 的值;
的值;
(2)从“满意”和“很满意”的人中随机抽取![]() 人,求至少有
人,求至少有![]() 人是“很满意”的概率.
人是“很满意”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月25日第23届冬季奥动会在韩国平昌闭幕,中国以![]() 金
金![]() 银
银![]() 铜的成绩结束本次冬奥会的征程,某校体育爱好者协会对某班进行了“本届冬奥会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),按分层抽样从该班学生中随机抽取了
铜的成绩结束本次冬奥会的征程,某校体育爱好者协会对某班进行了“本届冬奥会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),按分层抽样从该班学生中随机抽取了![]() 人,具体的调查结果如下表:
人,具体的调查结果如下表:
某班 | 满意 | 不满意 |
男生 |
|
|
女生 |
|
|
(1)若该班女生人数比男生人数多![]() 人,求该班男生人数和女生人数;
人,求该班男生人数和女生人数;
(2)若从该班调查对象的女生中随机选取![]() 人进行追踪调查,记选中的
人进行追踪调查,记选中的![]() 人中“满意”的人数为
人中“满意”的人数为![]() ,求
,求![]() 时对应事件的概率.
时对应事件的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com