
【题目】已知函数f(x)= ![]() .
.
(1)解不等式f(x)< ![]() ;
;
(2)求函数f(x)值域.
【答案】
(1)解:将f(x)的解析式代入不等式得:
![]() <
< ![]() ,
,
整理得:34x﹣3<4x+1,即4x=22x<2=21,
∴2x<1,
解得:x< ![]() ,
,
则不等式的解集为{x|x< ![]() }
}
(2)解:法一:f(x)= ![]() =1+
=1+ ![]() ,
,
∵4x>0,∴4x+1>1,
∴﹣2< ![]() <0,
<0,
∴﹣1<1+ ![]() <1,
<1,
则f(x)的值域为(﹣1,1);
法二:∵y=f(x)= ![]() ,
,
∴4x= ![]() >0,即
>0,即 ![]() <0,
<0,
可化为: ![]() 或
或 ![]() ,
,
解得:﹣1<y<1,
则f(x)的值域为(﹣1,1)
【解析】(1)把f(x)的解析式代入不等式,整理后得到关于4x的不等式,把不等式左右两边化为底数为2的幂形式,根据指数函数为增函数,得到关于x的不等式,求出不等式的解集即可得到原不等式的解集;(2)法一:把函数解析式整理为f(x)=1+ ![]() ,由4x大于0,得到4x+1的范围,可得到
,由4x大于0,得到4x+1的范围,可得到 ![]() 的范围,进而确定出1+
的范围,进而确定出1+ ![]() 的范围,即为函数f(x)的值域;
的范围,即为函数f(x)的值域;
法二:设y=f(x),从函数解析式中分离出4x , 根据4x大于0列出关于y的不等式,变形后得到y+1与y﹣1异号,转化为两个一元一次不等式,求出不等式的解集,即为函数的值域.
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】按照某学者的理论,假设一个人生产某产品单件成本为a元,如果他卖出该产品的单价为m元,则他的满意度为 ![]() ;如果他买进该产品的单价为n元,则他的满意度为
;如果他买进该产品的单价为n元,则他的满意度为 ![]() .如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2 , 则他对这两种交易的综合满意度为
.如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2 , 则他对这两种交易的综合满意度为 ![]() .现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为mAm元和mB元,甲买进A与卖出B的综合满意度为h甲 , 乙卖出A与买进B的综合满意度为h乙 .
.现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为mAm元和mB元,甲买进A与卖出B的综合满意度为h甲 , 乙卖出A与买进B的综合满意度为h乙 .
(1)求h甲和h乙关于mA、mB的表达式;当mA= ![]() mB时,求证:h甲=h乙;
mB时,求证:h甲=h乙;
(2)设mA= ![]() mB , 当mA、mB分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
mB , 当mA、mB分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入R(x)(万元)满足 ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)要使工厂有盈利,求产量x的范围;
(3)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=log2(2x+a)的定义域为(0,+∞).
(1)求a的值;
(2)若g(x)=log2(2x+1),且关于x的方程f(x)=m+g(x)在[1,2]上有解,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b. 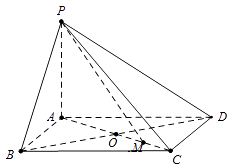
(1)求证:平面PBD⊥平面PAC;
(2)设AC与BD交于点O,M为OC中点,若二面角O﹣PM﹣D的正切值为2 ![]() ,求a:b的值.
,求a:b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com