
【题目】函数![]() 的一段图象过点(0,1),如图所示.
的一段图象过点(0,1),如图所示.

(1)求函数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得函数
个单位,得函数![]() 的图象,求
的图象,求![]() 的最大值,并求出此时自变量x的集合;
的最大值,并求出此时自变量x的集合;
(3)若![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() ;(2)2,
;(2)2,![]() ;(3)0.
;(3)0.
【解析】
(1)通过三个连续零点的值可以求出函数![]() 的周期,根据最小正周期公式可以求出
的周期,根据最小正周期公式可以求出![]() 的值,
的值,
根据图象平移的特点可以求出![]() 的值,再把点(0,1)的坐标代入解析式中,可以求出A的值;
的值,再把点(0,1)的坐标代入解析式中,可以求出A的值;
(2)根据正弦型函数的图象变换特点可以求出![]() 的解析式,结合正弦型函数的性质最后求出
的解析式,结合正弦型函数的性质最后求出![]() 的最大值,并求出此时自变量x的集合;
的最大值,并求出此时自变量x的集合;
(3)根据![]() 可求出
可求出![]() 的表达式,最后可以计算出
的表达式,最后可以计算出![]() 的值.
的值.
(1)由图知,T=π,于是ω=![]() =2.将y=Asin2x的图象向左平移
=2.将y=Asin2x的图象向左平移![]() ,
,
得y=Asin(2x+φ)的图象,于是φ=2·![]() =
=![]() .将(0,1)代入y=Asin(2x+
.将(0,1)代入y=Asin(2x+![]() ),得A=2.
),得A=2.
故![]() .
.
(2)依题意,f2(x)=2sin[2(x-![]() )+
)+![]() ]=-2cos(2x+
]=-2cos(2x+![]() ),
),
当2x+![]() =2kπ+π,即x=kπ+
=2kπ+π,即x=kπ+![]() (k∈Z)时,ymax=2.
(k∈Z)时,ymax=2.
x的取值集合为![]() .
.
(3)因为![]() ,所以
,所以![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的有________(只填序号)
①若直线与平面有无数个公共点,则直线在平面内;
②若直线l上有无数个点不在平面α内,则l∥α;
③若两条异面直线中的一条与一个平面平行,则另一条直线一定与该平面相交;
④若直线l与平面α平行,则l与平面α内的直线平行或异面;
⑤若平面α∥平面β,直线aα,直线bβ,则直线a∥b.
查看答案和解析>>
科目:高中数学 来源: 题型:
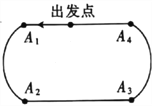
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子![]() 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子![]() 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过![]() 个直道与弯道的交接口
个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用![]() 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
(1)求该运动员停止滑行时恰好已顺利通过![]() 个交接口的概率;
个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题其中正确的有( )
A.“实数都大于0”的否定是“实数都小于或等于0”
B.“三角形外角和为360度”是含有全称量词的真命题
C.“至少存在一个实数![]() ,使得
,使得![]() ”是含有存在量词的真命题
”是含有存在量词的真命题
D.“能被3整除的整数,其各位数字之和也能被3整除”是全称量词命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
以这100台机器维修次数的频率代替1台机器维修次数发生的概率, 记![]() 表示1台机器三年内共需维修的次数,
表示1台机器三年内共需维修的次数,![]() 表示购买1台机器的同时购买的维修次数.
表示购买1台机器的同时购买的维修次数.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(3)以在维修上所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com