
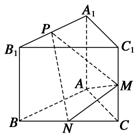
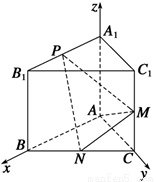
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直, AA1=AB=AC=1,AB⊥AC, M是CC1的中点, N是BC的中点,点P在线段A1B1上,且满足A1P=lA1B1.
(1)证明:PN⊥AM.
(2)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求该角最大值的正切值.
(3)是否存在点P,使得平面 PMN与平面ABC所成的二面角为45°.若存在求出l的值,若不存在,说明理由.
(1)见解析;(2)(tan θ)max=2;(3)不存在.
【解析】第一问中利用以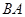 为
为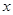 轴,
轴,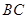 为
为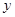 轴,
轴,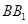 为
为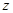 轴建立空间直角坐标系
轴建立空间直角坐标系
设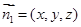 为平面
为平面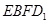 的法向量,又正方体的棱长为1,
的法向量,又正方体的棱长为1,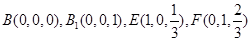
借助于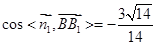 ,得到结论
,得到结论
第二问中,平面ABC的一个法向量为n=(0,0,1),
则sin θ=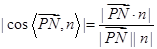 =
=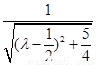 (*)
(*)
而θ∈[0,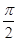 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=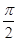 除外),
除外),
由(*)式,当λ=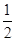 时,(sin θ)max=
时,(sin θ)max=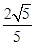 ,(tan
θ)max=2
,(tan
θ)max=2
第三问中,平面ABC的一个法向量为n 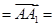 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),
由(1)得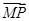 =(λ,-1,
=(λ,-1,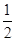 ).
).
由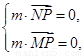 求出法向量,然后结合二面角得到解得λ=-
求出法向量,然后结合二面角得到解得λ=-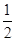 .
.
(1)证明 如图,以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz.则P(λ,0,1),N(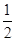 ,
,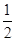 ,0),
,0),
从而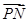 =(
=(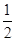 -λ,
-λ, 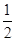 ,-1),
,-1),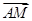 =(0,1,
=(0,1, 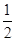 ).
).
\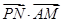 =(
=(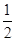 -λ)×0+
-λ)×0+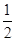 ×1-1×
×1-1×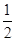 =0,
=0,
∴PN⊥AM. -------------4分
(2)解 平面ABC的一个法向量为n=(0,0,1),
则sin θ=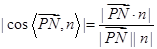 =
=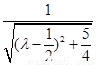 (*)
(*)
而θ∈[0,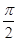 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=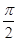 除外),
除外),
由(*)式,当λ=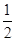 时,(sin θ)max=
时,(sin θ)max=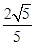 ,(tan
θ)max=2
-----------6分
,(tan
θ)max=2
-----------6分
(3)平面ABC的一个法向量为n 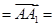 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),
由(1)得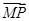 =(λ,-1,
=(λ,-1,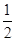 ).
).
由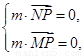
令x=3,得m=(3,2λ+1,2(1-λ)).
∵平面PMN与平面ABC所成的二面角为45°,
∴|cos〈m,n〉|=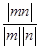 =
=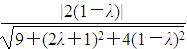 =
=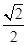 ,解得λ=-
,解得λ=-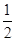 .
.
故在线段A1B1上不存在点P --------------6分


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,AB=2
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,AB=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足| A1P |
| A1B1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且| A1P |
| A1B1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com