
分析 根据同角三角函数关系式和万能公式化简后代入求值即可
解答 解:(1)$\frac{{{{sin}^2}(π+α)cos(π+α)}}{{tan(-α-2π)tan(π+α){{cos}^3}(-π-α)}}$
原式=$\frac{-si{n}^{2}α•cosα}{-tanα•tanα•(-co{s}^{3}α)}$=$\frac{-sinα•sinα•cosα}{\frac{sinα}{cosα}•\frac{sinα}{cosα}•co{s}^{3}α}$=-1
(2)已知sinα=-$\frac{4}{5}$,
那么:cosα=$±\sqrt{1-(-\frac{4}{5})^{2}}$=$±\frac{3}{5}$
∵α∈(-π,-$\frac{π}{2}$),
∴cosα=$-\frac{3}{5}$.
那么:tanα=$\frac{sinα}{cosα}=\frac{4}{3}$
则cosα+2tanα=$-\frac{3}{5}+2×\frac{4}{3}$=$\frac{31}{15}$.
点评 本题主要考察了同角三角函数关系式和万能公式的应用,属于基本知识的考查.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
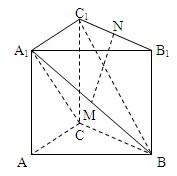 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3${\;}^{\frac{7}{8}}$ | B. | 3${\;}^{\frac{15}{8}}$ | C. | 3${\;}^{\frac{7}{4}}$ | D. | 3${\;}^{\frac{17}{8}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
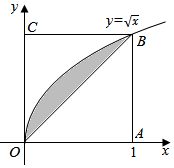 如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)等于( )
如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com