
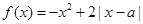 .
.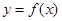 为偶函数,求
为偶函数,求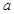 的值;
的值;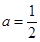 ,求函数
,求函数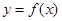 的单调递增区间;
的单调递增区间;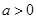 时,若对任意的
时,若对任意的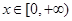 ,不等式
,不等式 恒成立,求实数
恒成立,求实数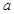 的取值范围.
的取值范围.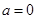 ;(2)
;(2)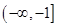 ,
,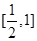 ;(3)
;(3)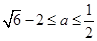 .
.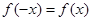 ,得到
,得到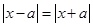 ,平方后可根据对应系数相等得到
,平方后可根据对应系数相等得到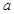 的值,也可将上式两边平方得
的值,也可将上式两边平方得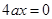 恒成立,得
恒成立,得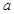 的值;(2)当
的值;(2)当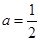 时,作出函数的图像,即可得到函数的单调递增区间;(3)先将不等式
时,作出函数的图像,即可得到函数的单调递增区间;(3)先将不等式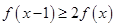 转化为
转化为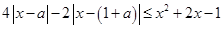 ,然后利用零点分段法(三段:
,然后利用零点分段法(三段: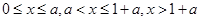 (
(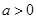 ))去掉绝对值,在每段上分别求解不等式的恒成立问题,可得出各段不等式恒成立时参数
))去掉绝对值,在每段上分别求解不等式的恒成立问题,可得出各段不等式恒成立时参数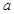 的取值范围,注意在后一段时可考虑结合前一段的参数
的取值范围,注意在后一段时可考虑结合前一段的参数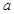 的取值范围进行求解,避免不必要的分类,最后对三段求出的
的取值范围进行求解,避免不必要的分类,最后对三段求出的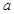 的取值范围取交集可得参数
的取值范围取交集可得参数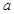 的取值范围.
的取值范围.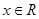 ,则
,则 恒成立
恒成立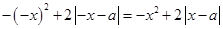 恒成立 3分
恒成立 3分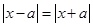 恒成立,两边平方得:
恒成立,两边平方得: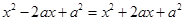
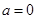 5分
5分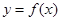 为偶函数,所以
为偶函数,所以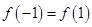 ,得
,得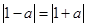 ,得:
,得: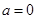 (酌情给分)
(酌情给分)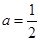 ,则
,则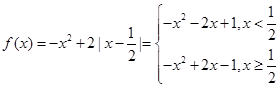 8分
8分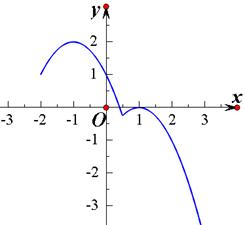
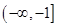 及
及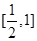 10分
10分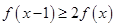 化为
化为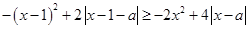
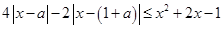 (*)对任意的
(*)对任意的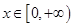 恒成立
恒成立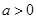 ,所以分如下情况讨论:
,所以分如下情况讨论: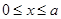 时,不等式(*)化为
时,不等式(*)化为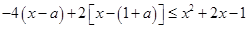
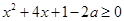 对任意的
对任意的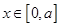 恒成立,
恒成立,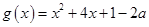 在区间
在区间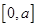 上单调递增,则只需
上单调递增,则只需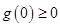 即可,得
即可,得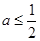 ,又
,又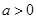
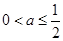 12分
12分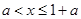 时,不等式(*)化为
时,不等式(*)化为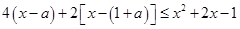 ,
,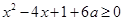 对任意的
对任意的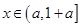 恒成立,
恒成立,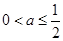 ,知:函数
,知:函数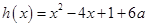 在区间
在区间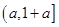 上单调递减,则只需
上单调递减,则只需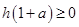 即可,即
即可,即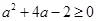 ,得
,得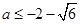 或
或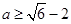
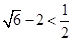 所以,由①得
所以,由①得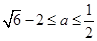 14分
14分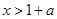 时,不等式(*)化为
时,不等式(*)化为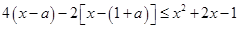
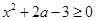 对任意的
对任意的 恒成立,
恒成立,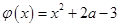 在区间
在区间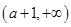 上单调递增,则只需
上单调递增,则只需 即可,
即可,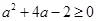 ,得
,得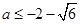 或
或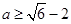 ,由②得
,由②得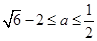
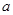 的取值范围是
的取值范围是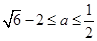 16分.
16分.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当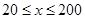 时,车流速度
时,车流速度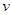 是车流密度x的一次函数.
是车流密度x的一次函数.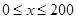 时,求函数
时,求函数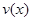 的表达式;
的表达式;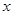 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com