
【题目】某车间20名工人年龄数据如表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(Ⅰ) 求这20名工人年龄的众数与平均数;
(Ⅱ) 以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(Ⅲ) 从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
【答案】解(Ⅰ) 由题意可知,这20名工人年龄的众数是30, 这20名工人年龄的平均数为 ![]() (19+3×28+3×29+5×30+4×31+3×32+40)=30,
(19+3×28+3×29+5×30+4×31+3×32+40)=30,
(Ⅱ) 这20名工人年龄的茎叶图如图所示:
(Ⅲ) 记年龄为24岁的三个人为A1 , A2 , A3;年龄为26岁的三个人为B1 , B2 , B3 ,
则从这6人中随机抽取2人的所有可能为
{A1 , A2},{A1 , A3},{A2 , A3},{A1 , B1},{A1 , B2},
{A1 , B3},{A2 , B1},{A2 , B2},{A2 , B , 3},{A3 , B1},
{A3 , B2},{A , 3 , B3},{B1 , B2},{B1 , B3},{B2 , B3}共15种.
满足题意的有{A1 , A2},{A1 , A3},{A2 , A3}3种,
故所求的概率为P= ![]()
【解析】(Ⅰ)利用车间20名工人年龄数据表能求出这20名工人年龄的众数和平均数.(Ⅱ)利用车间20名工人年龄数据表能作出茎叶图.(Ⅲ) 记年龄为24岁的三个人为A1 , A2 , A3;年龄为26岁的三个人为B1 , B2 , B3 , 利用列举法能求出这2人均是24岁的概率.
【考点精析】解答此题的关键在于理解茎叶图的相关知识,掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
【题目】△ABC中,若sinC=( ![]() cosA+sinA)cosB,则( )
cosA+sinA)cosB,则( )
A.B= ![]()
B.2b=a+c
C.△ABC是直角三角形
D.a2=b2+c2或2B=A+C
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系与直角坐标系xOy取相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知直线l的参数方程为 ![]() 为参数).曲线C的极坐标方程为
为参数).曲线C的极坐标方程为 ![]() .
.
(1)求直线l的倾斜角和曲线C的直角坐标方程;
(2)设直线C与曲线C交于A,B两点,与x轴的交点为M,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2分别是椭圆C: ![]() +y2=1的左、右焦点.
+y2=1的左、右焦点.
(1)若P是第一象限内该椭圆上的一点, ![]()
![]() =﹣
=﹣ ![]() ,求点P的坐标;
,求点P的坐标;
(2)设过定点M(0,2)的直线l与椭圆交于不同的两点A,B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() sinxcosx﹣sin2x,把f(x)的图象向右平移
sinxcosx﹣sin2x,把f(x)的图象向右平移 ![]() 个单位,再向上平移2个单位,得到y=g(x)的图象,若对任意实数x,都有g(α﹣x)=g(α+x)成立,则g(α+
个单位,再向上平移2个单位,得到y=g(x)的图象,若对任意实数x,都有g(α﹣x)=g(α+x)成立,则g(α+ ![]() )+g(
)+g( ![]() )=( )
)=( )
A.4
B.3
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 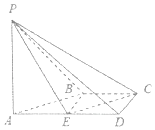
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求二面角P﹣CE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣6x2+9x,g(x)= ![]() x3﹣
x3﹣ ![]() x2+ax﹣
x2+ax﹣ ![]() (a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
(a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
A.(1, ![]() ]??
]??
B.[9,+∞)??
C.(1, ![]() ]∪[9,+∞)??
]∪[9,+∞)??
D.[ ![]() ,
, ![]() ]∪[9,+∞)
]∪[9,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com