
| A. | [-1,1] | B. | [0,1] | C. | {-1}∪(0,1] | D. | {-1}∪[0,1) |
分析 根据函数和方程之间的关系讲方程转化为aex-1-1=-|x-a|,利用数形结合分别作出函数t(x)=aex-1-1与g(x)=-|x-a|的图象,利用数形结合进行求解即可.
解答 解:由f(x)=aex-1+|x-a|-1=0,得aex-1-1=-|x-a|,
设g(x)=-|x-a|,t(x)=aex-1-1,
①若a=0,则t(x)=-1,g(x)=-|x|,
作出t(x)和g(x)的图象如图:此时两个函数有两个交点,满足条件,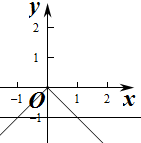
②若a>0,则函数g(x)的零点为(a,0),
由t(x)=0得aex-1-1=0,即ex-1=$\frac{1}{a}$,
则x-1=ln$\frac{1}{a}$=-lna,
则x=1-lna,
即f(x)的零点为(1-lna,0),
若两个函数有两个零点,
则1-lna>a,即1-lna-a>0,
设h(a)=1-lna-a,则函数在(0,+∞)上为减函数,
∵h(1)=1-ln1-1=0,
∴由h(a)>0得h(a)>h(1),得a<1.
即此时0<a<1,
③若a<0,当x>a时,g(x)=-|x-a|=-x+a,
当g(x)与t(x)相切时,满足有两个交点,
此时t′(x)=aex-1,设切点为(m,n),
则切线斜率k=aem-1,n=aem-1-1,即切点坐标为(m,aem-1-1),
则切线方程为y-(aem-1-1)=aem-1(x-m),
即y=aem-1(x-m)+(aem-1-1)=aem-1•x-maem-1+aem-1-1,
∵g(x)=-x+a
∴aem-1=-1,-maem-1+aem-1-1=a,
得m-1-1=a,即m=a+2,
则aea+2-1=-1,即aea+1=-1,
得a=-1,
综上所述,0≤a<1或a=-1
故选:D.
点评 本题主要考查根的个数的判断,根据函数与方程的关系,转化为两个函数的交点问题,利用分类讨论的数学思想进行求解即可,综合性较强,难度大.


科目:高中数学 来源: 题型:选择题

| A. | f(x)=lnx-sinx | B. | f(x)=lnx+cosx | C. | f(x)=lnx+sinx | D. | f(x)=lnx-cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于x轴对称的图形 | B. | 关于y轴对称的图形 | ||
| C. | 关于原点对称的图形 | D. | 关于直线y=x对称的图形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数y=loga(x+b)(a,b为常数)的图象如图所示,则函数g(x)=b${\;}^{{x}^{2}-2x}$,x∈[0,3]的最大值是( )
已知函数y=loga(x+b)(a,b为常数)的图象如图所示,则函数g(x)=b${\;}^{{x}^{2}-2x}$,x∈[0,3]的最大值是( )| A. | 1 | B. | b | C. | b2 | D. | $\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥S-ABCD,SB⊥AD,侧面SAD是边长为4的等边三角形,底面ABCD为菱形,侧面SAD与底面ABCD所成的二面角为120°.
如图,已知四棱锥S-ABCD,SB⊥AD,侧面SAD是边长为4的等边三角形,底面ABCD为菱形,侧面SAD与底面ABCD所成的二面角为120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | 2-a<2-b | C. | a2>b2 | D. | ac≥bc |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com