
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为![]() (
(![]() 为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=
为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=![]() 时,这两个交点重合.
时,这两个交点重合.
(1) 求曲线C1,C2的直角坐标方程
(2) 设当 α=![]() 时,l与C1,C2的交点分别为A1,B1,当 α=-
时,l与C1,C2的交点分别为A1,B1,当 α=-![]() 时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
【答案】(1)C1,C2的普通方程分别为x2+y2=1和![]() +y2=1,(2)
+y2=1,(2)![]()
【解析】
(1)令α=0和α=![]() 得a,b 值由参数方程与普通方程的互化求解得C1,C2的普通方程;(2)令α=
得a,b 值由参数方程与普通方程的互化求解得C1,C2的普通方程;(2)令α=![]() ,得A1,B1的横坐标,利用对称性得A1,B1关于x轴对称,得四边形A1A2B2B1为等腰梯形,利用面积公式求解即可
,得A1,B1的横坐标,利用对称性得A1,B1关于x轴对称,得四边形A1A2B2B1为等腰梯形,利用面积公式求解即可
由题C1 的普通方程为x2+y2=1;C2的普通方程为![]()
当α=0时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),因为这两点间的距离为2,所以a=3.
当α=![]() 时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
故C1,C2的普通方程分别为x2+y2=1和![]() +y2=1,
+y2=1,
(2)当α=![]() 时,射线l与C1交点A1的横坐标为x=
时,射线l与C1交点A1的横坐标为x=![]() ,与C2交点B1的横坐标为x′=
,与C2交点B1的横坐标为x′=![]() .
.
当α=-![]() 时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此四边形A1A2B2B1为梯形.
时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此四边形A1A2B2B1为梯形.
故四边形A1A2B2B1的面积为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某地区发现某污染源,相关部门对污染情况进行调查研究后,发现一天中污染指数![]() 与时刻x(时)的函数关系为
与时刻x(时)的函数关系为![]() ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且![]() .按规定,若每天污染指数不超过2,则环保合格,否则需要整改.如果以每天中
.按规定,若每天污染指数不超过2,则环保合格,否则需要整改.如果以每天中![]() 的最大值作为当天的污染指数,并记为
的最大值作为当天的污染指数,并记为![]() ,那么该地区污染指数的超标情况为________.
,那么该地区污染指数的超标情况为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数图象的有下列说法:
①若函数![]() 满足
满足![]() ,则
,则![]() 的一个周期为
的一个周期为![]() ;
;
②若函数![]() 满足
满足![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④若函数![]() 与函数
与函数![]() 的图象关于原点对称,则
的图象关于原点对称,则![]() ,
,
其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药开发公司实验室有![]() 瓶溶液,其中
瓶溶液,其中![]() 瓶中有细菌
瓶中有细菌![]() ,现需要把含有细菌
,现需要把含有细菌![]() 的溶液检验出来,有如下两种方案:
的溶液检验出来,有如下两种方案:
方案一:逐瓶检验,则需检验![]() 次;
次;
方案二:混合检验,将![]() 瓶溶液分别取样,混合在一起检验,若检验结果不含有细菌
瓶溶液分别取样,混合在一起检验,若检验结果不含有细菌![]() ,则
,则![]() 瓶溶液全部不含有细菌
瓶溶液全部不含有细菌![]() ;若检验结果含有细菌
;若检验结果含有细菌![]() ,就要对这
,就要对这![]() 瓶溶液再逐瓶检验,此时检验次数总共为
瓶溶液再逐瓶检验,此时检验次数总共为![]() .
.
(1)假设![]() ,采用方案一,求恰好检验3次就能确定哪两瓶溶液含有细菌
,采用方案一,求恰好检验3次就能确定哪两瓶溶液含有细菌![]() 的概率;
的概率;
(2)现对![]() 瓶溶液进行检验,已知每瓶溶液含有细菌
瓶溶液进行检验,已知每瓶溶液含有细菌![]() 的概率均为
的概率均为![]() .
.
若采用方案一.需检验的总次数为![]() ,若采用方案二.需检验的总次数为
,若采用方案二.需检验的总次数为![]() .
.
(i)若![]() 与
与![]() 的期望相等.试求
的期望相等.试求![]() 关于
关于![]() 的函数解析式
的函数解析式![]() ;
;
(ii)若![]() ,且采用方案二总次数的期望小于采用方案一总次数的期望.求
,且采用方案二总次数的期望小于采用方案一总次数的期望.求![]() 的最大值.
的最大值.
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地举办水果观光采摘节,并推出配套旅游项目,统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图.
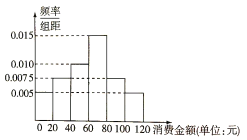
(1)若将消费金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;
(2)从(1)中的5人中抽取2人作为幸运客户免费参加配套旅游项目,请列出所有的可能结果,并求这2人中至少有1人购买金额不低于100元的概率;
(3)为吸引顾客,该地特推出两种促销方案,
方案一:每满80元可立减8元;
方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.
若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查,得到了如下的统计结果:

(1)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(2)完成联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”.

附:![]() ,其中n=a+b+c+d为样本容量.
,其中n=a+b+c+d为样本容量.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过原点
,过原点![]() 且斜率为1的直线
且斜率为1的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,四边形
两点,四边形![]() 的周长与面积分别为8与
的周长与面积分别为8与![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,求证:
,求证:![]() 到直线
到直线![]() 的距离为定值.
的距离为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com