
【题目】已知函数f(x)定义在区间(﹣1,1)内,对于任意的x,y∈(﹣1,1)有f(x)+f(y)=f( ![]() ),且当x<0时,f(x)>0.
),且当x<0时,f(x)>0.
(1)判断这样的函数是否具有奇偶性和单调性,并加以证明;
(2)若f(﹣ ![]() )=1,求方程f(x)+
)=1,求方程f(x)+ ![]() =0的解.
=0的解.
【答案】
(1)解:令x=y=0,则f(0)=0,令y=﹣x,则f(x)+f(﹣x)=0,
即f(﹣x)=﹣f(x),即函数f(x)为奇函数.
任取x1,x2∈(﹣1,1),且x1<x2,则f(x1)﹣f(x2)=f(x1)+f(﹣x2)=f( ![]() ).
).
﹣1<x1<x2<1,可得﹣1<x1x2<,则 ![]() <10,则f(
<10,则f( ![]() )>0,
)>0,
即f(x1)>f(x2).则f(x)在区间(﹣1,1)内是减函数
(2)解:f(x)为奇函数,则f( ![]() )=﹣1,
)=﹣1,
又2f(x)=f(x)+f(x)=f( ![]() ),且f(x)+
),且f(x)+ ![]() =0,
=0,
即2f(x)+1=0,2f(x)=﹣1.则f( ![]() )=f(
)=f( ![]() ).
).
f(x)在区间(﹣1,1)内是单调函数,
可得 ![]() =
= ![]() .
.
即x=2﹣ ![]() 或x=2+
或x=2+ ![]() (舍).
(舍).
故方程的解为2﹣ ![]()
【解析】(1)分别令x=y=0,求得f(0)=0,令y=﹣x,结合奇偶性定义即可判断;再由单调性的定义,即可得到f(x)在区间(﹣1,1)内是减函数;(2)运用奇函数的定义,可令y=x,结合单调性,可得方程 ![]() =
= ![]() ,即可得到方程的解.
,即可得到方程的解.
【考点精析】认真审题,首先需要了解函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较),还要掌握函数的奇偶性(偶函数的图象关于y轴对称;奇函数的图象关于原点对称)的相关知识才是答题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】在高校自主招生中,某学校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1名.并且北京大学和清华大学都要求必须有男生参加.学校通过选拔定下3男2女共5个推荐对象,则不同的推荐方法共有( )
A.20种
B.22种
C.24种
D.36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,E是矩形ABCD中AD边上的点,F是CD上的点,AB=AE= ![]() AD=4,现将△ABE沿BE边折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF.
AD=4,现将△ABE沿BE边折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF. 
(1)求 ![]() 的比值;
的比值;
(2)求二面角E﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若y=f(x)=Asin(ωx+φ)(A>0,ω>0, ![]() 的部分图象如图所示.
的部分图象如图所示. 
(I)求函数y=f(x)的解析式;
(II)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象;若y=g(x)图象的一个对称中心为 ![]() ,求θ的最小值.
,求θ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() 满足|
满足| ![]() |=|
|=| ![]() =1,且|k
=1,且|k ![]() +
+ ![]() |=
|= ![]() |
| ![]() ﹣k
﹣k ![]() |(k>0),令f(k)=
|(k>0),令f(k)= ![]()
![]() . (Ⅰ)求f(k)=
. (Ⅰ)求f(k)= ![]()
![]() (用k表示);
(用k表示);
(Ⅱ)若f(k)≥x2﹣2tx﹣ ![]() 对任意k>0,任意t∈[﹣1,1]恒成立,求实数x的取值范围.
对任意k>0,任意t∈[﹣1,1]恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足g(3)=8,又定义域为实数集R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)讨论函数y=f(x)的单调性;
(2)若对任意的t∈R,不等式f(2t﹣3t2)+f(t2﹣k)>0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn=2an﹣a1 , 且a1 , a2+1,a3成等差数列.
(1)求数列{an}的通项公式;
(2)记数列 ![]() 的前n项和Tn , 求使得
的前n项和Tn , 求使得 ![]() 成立的n的最小值.
成立的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m 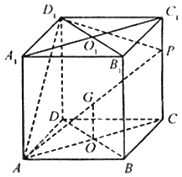
(1)试确定m,使直线AP与平面BDD1B1所成角的正切值为 ![]() ;
;
(2)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com