
【题目】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
【答案】C
【解析】解:∵抛物线C方程为y2=2px(p>0),
∴焦点F坐标为(![]() , 0),可得|OF|=
, 0),可得|OF|=![]() ,
,
∵以MF为直径的圆过点(0,2),
∴设A(0,2),可得AF⊥AM,
Rt△AOF中,|AF|=![]()
∴sin∠OAF=
∵根据抛物线的定义,得直线AO切以MF为直径的圆于A点,
∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF=
∵|MF|=5,|AF|=![]()
∴ ,整理得
,整理得![]() ,解之可得p=2或p=8
,解之可得p=2或p=8
因此,抛物线C的方程为y2=4x或y2=16x.
故选:C.
方法二:
∵抛物线C方程为y2=2px(p>0),∴焦点F(![]() , 0),
, 0),
设M(x,y),由抛物线性质|MF|=x+![]() =5,可得x=5﹣
=5,可得x=5﹣![]() ,
,
因为圆心是MF的中点,所以根据中点坐标公式可得,圆心横坐标为![]()
由已知圆半径也为![]() , 据此可知该圆与y轴相切于点(0,2),故圆心纵坐标为2,则M点纵坐标为4,
, 据此可知该圆与y轴相切于点(0,2),故圆心纵坐标为2,则M点纵坐标为4,
即M(5﹣![]() , 4),代入抛物线方程得p2﹣10p+16=0,所以p=2或p=8.
, 4),代入抛物线方程得p2﹣10p+16=0,所以p=2或p=8.
所以抛物线C的方程为y2=4x或y2=16x.
故答案C.
根据抛物线方程算出|OF|=![]() , 设以MF为直径的圆过点A(0,2),在Rt△AOF中利用勾股定理算出|AF|=
, 设以MF为直径的圆过点A(0,2),在Rt△AOF中利用勾股定理算出|AF|=![]() .再由直线AO与以MF为直径的圆相切得到∠OAF=∠AMF,Rt△AMF中利用∠AMF的正弦建立关系式,从而得到关于p的方程,解之得到实数p的值,进而得到抛物线C的方程.
.再由直线AO与以MF为直径的圆相切得到∠OAF=∠AMF,Rt△AMF中利用∠AMF的正弦建立关系式,从而得到关于p的方程,解之得到实数p的值,进而得到抛物线C的方程.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的参数方程为 (θ是参数),直线l的极坐标方程为
(θ是参数),直线l的极坐标方程为![]() (ρ∈R)
(ρ∈R)
(Ⅰ)求C的普通方程与极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax2﹣2ax+b(a≠0)在闭区间[1,2]上有最大值0,最小值﹣1,则a,b的值为( )
A.a=1,b=0
B.a=﹣1,b=﹣1
C.a=1,b=0或a=﹣1,b=﹣1
D.以上答案均不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知c>0,设命题p:函数y=cx为减函数;命题q:当x∈[![]() , 2]时,函数f(x)=x+
, 2]时,函数f(x)=x+![]() >
>![]() 恒成立,如果p∨q为真命题,p∧q为假命题,求c的取值范围.
恒成立,如果p∨q为真命题,p∧q为假命题,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
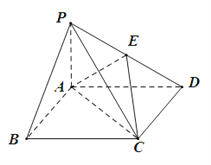
【题目】如图,四棱锥P ABCD中,底面ABCD为平行四边形, ![]() ,PA⊥平面ABCD,E为PD的中点.
,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设AD=2, ![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE= ![]() AD,
AD, 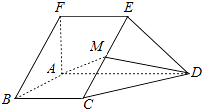
(1)求异面直线BF与DE所成的角的大小;
(2)证明平面AMD⊥平面CDE;
(3)求二面角A﹣CD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+a2(a>0)在x=1处有极值10.
(1)求a、b的值;
(2)求f(x)的单调区间;
(3)求f(x)在[0,4]上的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com