Question

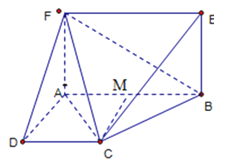
【题目】如图，已知 AF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=2，AB=4．
（I）求证：AC⊥平面BCE；
（II）求三棱锥E﹣BCF的体积．

Answer 1

【答案】（I）证明：过C作CM⊥AB，垂足为M，
∵AD⊥DC，∴四边形ADCM为矩形，
∴AM=MB=2，
∵AD=2，AB=4，
∴AC=2，CM=2，BC=2
∴AB2=AC2+BC2 ， 即AC⊥BC，
∵AF⊥平面ABCD，AF∥BE，
∴EB⊥平面ABCD，
∵AC平面ABCD，∴AC⊥EB，
∵EB∩BC=B，
∴AC⊥平面BCE；
（II）解：∵AF⊥平面ABCD，
∴AF⊥CM，
∴CM⊥AB，AB∩AF=A，
∴CM⊥平面ABEF，
∴VE﹣BCF=VC﹣BEF=xBEXEFXCM=X2X4X2=．

【解析】（I）过C作CM⊥AB，垂足为M，利用勾股定理证明AC⊥BC，利用EB⊥平面ABCD，证明AC⊥EB，即可证明AC⊥平面BCE；
（II）证明CM⊥平面ABEF，利用VE﹣BCF=VC﹣BEF ， 即可求三棱锥E﹣BCF的体积．
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．