
【题目】广元市某校高三数学备课组为了更好地制定二轮复习的计划,开展了试卷讲评后效果的调研,从上学期市一诊考试数学试题中选出一些学生易错题,重新进行测试,并认为做这些题不出任何错误的同学为“过关”,出了错误的同学为“不过关”,现随机抽查了年级![]() 人,他们的测试成绩的频数分布如下表:
人,他们的测试成绩的频数分布如下表:
市一诊分数段 |
|
|
|
|
|
人数 | 5 | 10 | 15 | 13 | 7 |
“过关”人数 | 1 | 3 | 8 | 8 | 6 |
(1)由以上统计数据完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为市一诊数学成绩不低于
的把握认为市一诊数学成绩不低于![]() 分与测试“过关”有关?说明你的理由;
分与测试“过关”有关?说明你的理由;
分数低于 | 分数不低于 | 合计 | |
“过关”人数 | |||
“不过关”人数 | |||
合计 |
(2)根据以上数据估计该校市一诊考试数学成绩的中位数.下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
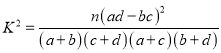
【答案】(1)填表见解析;有![]() 的把握认为期末数学成绩不低于
的把握认为期末数学成绩不低于![]() 分与测试“过关”有关,详见解析(2)中位数为
分与测试“过关”有关,详见解析(2)中位数为![]() 分
分
【解析】
(1)首先根据频数分布表中的数据填![]() 列联表,然后计算出
列联表,然后计算出![]() 即可;
即可;
(2)算出每个分数段的频率,然后即可算出中位数.
(1)根据题意得![]() 列联表如下:
列联表如下:
分数低于 | 分数不低于 | 合计 | |
“过关”人数 | 12 | 14 | 26 |
“不过关”人数 | 18 | 6 | 24 |
合计 | 30 | 20 | 50 |
所以,![]() .
.
因此有![]() 的把握认为期末数学成绩不低于
的把握认为期末数学成绩不低于![]() 分与测试“过关”有关.
分与测试“过关”有关.
(2)设该市一诊考试数学成绩的中位数为![]() .
.
市一诊分数段 |
|
|
|
|
|
人数 | 5 | 10 | 15 | 13 | 7 |
频率 | 0.1 | 0.2 | 0.3 | 0.26 | 0.14 |
根据题意有:![]() ,
,
解得:![]() .
.
所以,该校市一诊考试数学成绩的中位数为![]() 分.
分.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前n项
的前n项![]() ,
,![]() ,…,
,…,![]() 的最大项为
的最大项为![]() ,第n项之后的各项
,第n项之后的各项![]() ,
,![]() ,…的最小项为
,…的最小项为![]() ,
,![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,写出
,写出![]() ,
,![]() ,
,![]() ;
;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,判断
,判断![]() 是否为等差数列,若是,求出公差;若不是,请说明理由;
是否为等差数列,若是,求出公差;若不是,请说明理由;
(3)若数列![]() 为公差大于零的等差数列,求证:
为公差大于零的等差数列,求证:![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 对任意的
对任意的![]() 都有
都有![]() ,且
,且![]() 时
时![]() 的最大值为
的最大值为![]() ,下列四个结论:①
,下列四个结论:①![]() 是
是![]() 的一个极值点;②若
的一个极值点;②若![]() 为奇函数,则
为奇函数,则![]() 的最小正周期
的最小正周期![]() ;③若
;③若![]() 为偶函数,则
为偶函数,则![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() .其中一定正确的结论编号是( )
.其中一定正确的结论编号是( )
A.①②B.①③C.①②④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由边长为4的正六边形![]() ,矩形
,矩形![]() ,组成的一个平面图形,将其沿
,组成的一个平面图形,将其沿![]() ,
,![]() 折起得几何体
折起得几何体![]() ,使得
,使得![]() ,且平面
,且平面![]() 平面
平面![]() ,如图2.
,如图2.
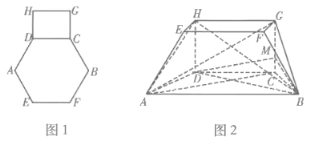
(1)证明:图2中,平面![]() 平面
平面![]() ;
;
(2)设点M为图2中线段![]() 上一点,且
上一点,且![]() ,若直线
,若直线![]() 平面
平面![]() ,求图2中的直线
,求图2中的直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业批量生产了一种汽车配件,总数为![]() ,配件包装上标有从1到
,配件包装上标有从1到![]() 的连续自然数序号,为对配件总数
的连续自然数序号,为对配件总数![]() 进行估计,质检员随机抽取了
进行估计,质检员随机抽取了![]() 个配件,序号从小到大依次为
个配件,序号从小到大依次为![]() ,
,![]() ,…,
,…,![]() ,这
,这![]() 个序号相当于从区间
个序号相当于从区间![]() 上随机抽取了
上随机抽取了![]() 个整数,这
个整数,这![]() 个整数将区间
个整数将区间![]() 分为
分为![]() 个小区间
个小区间![]() ,
,![]() ,…,
,…,![]() .由于这
.由于这![]() 个整数是随机抽取的,所以前
个整数是随机抽取的,所以前![]() 个区间的平均长度
个区间的平均长度![]() 与所有
与所有![]() 个区间的平均长度
个区间的平均长度![]() 近似相等,进而可以得到
近似相等,进而可以得到![]() 的估计值.已知
的估计值.已知![]() ,质检员随机抽取的配件序号从小到大依次为83,135,274,…,3104.
,质检员随机抽取的配件序号从小到大依次为83,135,274,…,3104.
(1)用上面的方法求![]() 的估计值.
的估计值.
(2)将(1)中的![]() 估计值作为这批汽车配件的总数,从中随机抽取100个配件测量其内径
估计值作为这批汽车配件的总数,从中随机抽取100个配件测量其内径![]() (单位:
(单位:![]() ),绘制出频率分布直方图如下:
),绘制出频率分布直方图如下:
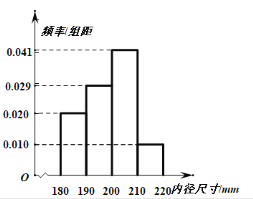
将这100个配件的内径落入各组的频率视为这![]() 个配件内径分布的概率,已知标准配件的内径为200
个配件内径分布的概率,已知标准配件的内径为200![]() ,把这
,把这![]() 个配件中内径长度最接近标准配件内径长度的800个配件定义为优等品,求优等品配件内径
个配件中内径长度最接近标准配件内径长度的800个配件定义为优等品,求优等品配件内径![]() 的取值范围(结果保留整数).
的取值范围(结果保留整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F是抛物线C:x2=4y的焦点,过E(0,﹣1)的直线l与抛物线分別交于A,B两点.
(1)设直线AF,BF的斜率分別为k1,k2,证明:k1+k2=0;
(2)若![]() 的面积为
的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com